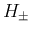
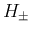 は、前節の拡張版も含め
は、前節の拡張版も含め 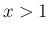 (
(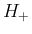 ),
), 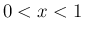 (
(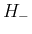 ) で
は明らかに滑らかな関数だから、その可積分性や有界性は、
境界の評価、すなわち収束 order のみによって決まる。
本節以降、
) で
は明らかに滑らかな関数だから、その可積分性や有界性は、
境界の評価、すなわち収束 order のみによって決まる。
本節以降、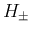 の境界の評価を考える。
まずは
の境界の評価を考える。
まずは 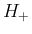 の
の
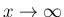 の評価から。
の評価から。
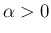 ,
, 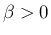 に対して、
に対して、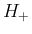 を
を
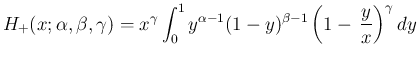
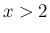 なら
なら 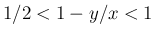 より
より
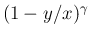 は有界なので、
は有界なので、
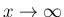 に対して
ルベーグ収束定理により
に対して
ルベーグ収束定理により
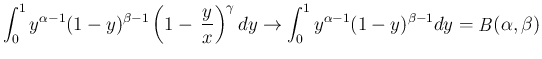
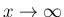 に対しては、
となる。
に対しては、
となる。
よって、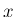 が
が 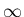 の近くでは、
の近くでは、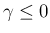 の場合に
の場合に 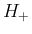 は
有界で、
は
有界で、
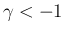 の場合に
の場合に 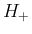 は可積分であることになる。
は可積分であることになる。
竹野茂治@新潟工科大学