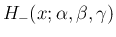
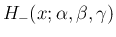 を、
を、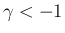 なる
非整数の
なる
非整数の 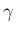 に拡張することを考える。
に拡張することを考える。
まず、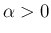 ,
, 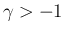 に対して、
に対して、
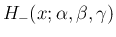 を
を
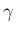 が 1 つ大きい
が 1 つ大きい 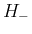 で表す。
以後簡単のため、
で表す。
以後簡単のため、
[i]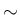 [v] の性質は、この記号を使うと以下のように書ける。
[v] の性質は、この記号を使うと以下のように書ける。
![$\displaystyle \begin{array}{cl}
\mathrm{[i]} &
[0,0,1]' = (\gamma+1)[0,0,0]\\...
...
\mathrm{[v]} &
(\gamma+1)[1,1,0]-\alpha[0,1,1]+\beta[1,0,1]=0
\end{array}$](img43.png)
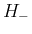 では
では 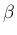 は小さくても構わないので、[v] で
は小さくても構わないので、[v] で 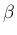 を一つ下げ
ると
を一つ下げ
ると
![$\displaystyle (\gamma+1)[1,0,0]_{-}-\alpha[0,0,1]_{-}+(\beta-1)[1,-1,1]_{-}=0
$](img44.png)
![$\displaystyle (\gamma+1)(x[0,0,0]_{-}-[0,0,1]_{-})=\alpha[0,0,1]_{-}-(\beta-1)[1,-1,1]_{-}
$](img45.png)
![$[0,0,0]_{-}$](img47.png) を一つ大きい
を一つ大きい 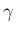 の
の 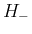 を用いて表せる。
これは、
を用いて表せる。
これは、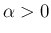 ,
, 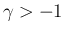 で非整数の
で非整数の
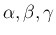 すべてに対して成立するが、
逆にこれを用いて、
すべてに対して成立するが、
逆にこれを用いて、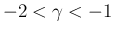 に対する
に対する
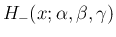 を
定義することにする。すなわち
を
定義することにする。すなわち 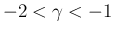 に対して、
に対して、
これにより、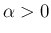 ,
, 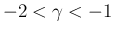 に対する
に対する 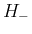 が定まり、
そしてそれにより、再び (10) を用いることにより、
が定まり、
そしてそれにより、再び (10) を用いることにより、
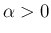 ,
, 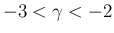 に対する
に対する 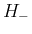 を定義することができ、
この手続きを繰り返すことによって、
を定義することができ、
この手続きを繰り返すことによって、
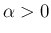 ,
, 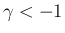 を満たす任意の非整数の
を満たす任意の非整数の
 に対する
に対する  を
を 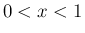 で定義できることがわかる。
で定義できることがわかる。
この 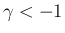 に拡張された
に拡張された 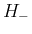 に対し、再び [i]
に対し、再び [i]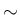 [v] が
成り立つことを次に示す。
[v] が
成り立つことを次に示す。
まず [i] から。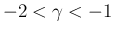 とする。この場合は、(9) より
とする。この場合は、(9) より
そにれは、まず左辺の ![$[0,0,1]_{-}$](img55.png) に (9) を用いて、
に (9) を用いて、
![$\displaystyle x[0,0,1]_{-} = \frac{\alpha+\gamma+2}{\gamma+2}[0,0,2]_{-}
-\,\frac{\beta-1}{\gamma+2}[1,-1,2]_{-}
$](img56.png)
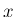 で微分すると
で微分すると
![$\displaystyle [0,0,1]_{-} +x[0,0,1]_{-}' = \frac{\alpha+\gamma+2}{\gamma+2}[0,0,2]_{-}'
-\,\frac{\beta-1}{\gamma+2}[1,-1,2]_{-}'
$](img58.png)
![$\displaystyle [0,0,1]_{-} + x[0,0,1]_{-}' = (\alpha+\gamma+2)[0,0,1]_{-}
-(\beta-1)[1,-1,1]_{-}
$](img59.png)
![$\displaystyle x[0,0,1]_{-}' = (\alpha+\gamma+1)[0,0,1]_{-} -(\beta-1)[1,-1,1]_{-}
$](img60.png)
この証明では、一つ小さい 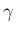 を定義する式 (9) と [i] を用いているだけなので、
これはそのまま
を定義する式 (9) と [i] を用いているだけなので、
これはそのまま 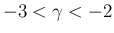 の場合にも用いることができ、
よってこれで帰納的に
の場合にも用いることができ、
よってこれで帰納的に 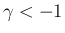 のすべての非整数の
のすべての非整数の 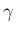 で [i] が成立することになる。
で [i] が成立することになる。
さらにこの証明を振り返ると、実質的に 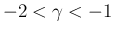 であることは
使っておらず、[i]
であることは
使っておらず、[i] [v] の性質のみを用いていることがわかる。
すなわち、
[v] の性質のみを用いていることがわかる。
すなわち、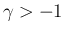 に対してはすでに成り立つことが
知られている式に対して当然成立する機械的な計算を行っているだけであり、
その同じ計算を、機械的に
に対してはすでに成り立つことが
知られている式に対して当然成立する機械的な計算を行っているだけであり、
その同じ計算を、機械的に 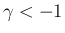 の場合の証明に用いている
形になっていて、行われる式変形は両者で全く違わない。
の場合の証明に用いている
形になっていて、行われる式変形は両者で全く違わない。
[i] 以外の [ii]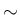 [v] の性質の証明もこれと同じで、
その証明は [ii]
[v] の性質の証明もこれと同じで、
その証明は [ii]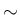 [v] を用いた式変形のみで、
[v] を用いた式変形のみで、
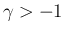 で成立する計算と全く同じ式変形を
で成立する計算と全く同じ式変形を 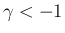 に対して
実行するだけであり、よって
に対して
実行するだけであり、よって 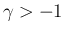 と同じ結論が
自然に
と同じ結論が
自然に 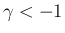 でも得られることになり、
これで
でも得られることになり、
これで 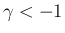 でも成り立つことが保証される。
でも成り立つことが保証される。
なお、この一見手抜きにも見える証明は、数学では本来複素関数論の分野の
「解析接続」という手法で正当化されるもので、
本稿の 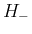 の
の 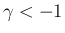 への拡張自体がその「解析接続」に
なるのであるが、本稿では
への拡張自体がその「解析接続」に
なるのであるが、本稿では 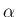 ,
, 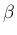 ,
, 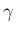 は実数値の場合しか
扱わないので、表面上「解析接続」は用いずに「(9) に
よって拡張する」という言い方をしておく。
は実数値の場合しか
扱わないので、表面上「解析接続」は用いずに「(9) に
よって拡張する」という言い方をしておく。
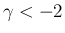 に対する
に対する  は、(9) を
繰り返し用いることで帰納的に定義したが、
実際に (9) を繰り返して得られる公式を一つ紹介する。
は、(9) を
繰り返し用いることで帰納的に定義したが、
実際に (9) を繰り返して得られる公式を一つ紹介する。
任意の自然数 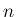 に対し、
に対し、
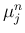 は以下の通り。
は以下の通り。
証明
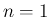 の場合は (12),(13) は容易に
(9) に一致することがわかる。
の場合は (12),(13) は容易に
(9) に一致することがわかる。
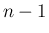 で (12),(13) が成立するとすると、
で (12),(13) が成立するとすると、
![$\displaystyle x[j,-j,n-1] = \frac{\alpha+\gamma+j+n}{\gamma+n}[j,-j,n]
-\,\frac{\beta-j-1}{\gamma+n}[j+1,-j-1,n]
$](img69.png)
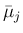 は
となる。なお、
は
となる。なお、
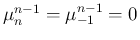 とする。
あとはこの
とする。
あとはこの 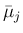 が
が 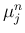 に一致することを示せばよい。
に一致することを示せばよい。
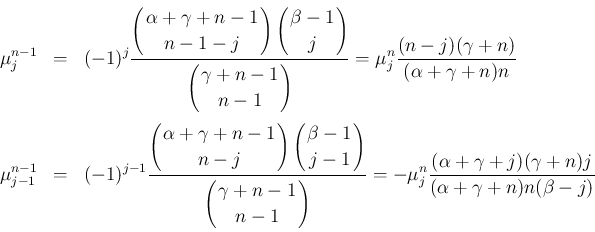
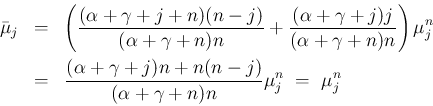
この補題 2 を用いれば、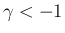 の
の  は
帰納的に考えなくても一度で
は
帰納的に考えなくても一度で 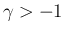 に対する
に対する 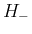 、
すなわち積分を用いた式で表すことができる。
逆に言えば、
、
すなわち積分を用いた式で表すことができる。
逆に言えば、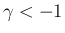 に拡張した
に拡張した 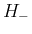 は、
実際には (12) の右辺の式で表されるものを
意味することになる。
は、
実際には (12) の右辺の式で表されるものを
意味することになる。
竹野茂治@新潟工科大学