3.5
 の評価: [A-1] の場合
の評価: [A-1] の場合
 の評価: [A-1] の場合
の評価: [A-1] の場合
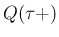 と
と 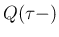 で
で 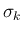 ,
, 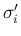 ,
, 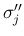 が
含まれない項は当然共通しているため、その差では消えてしまうので、
残るのは、
が
含まれない項は当然共通しているため、その差では消えてしまうので、
残るのは、
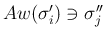 ,
,
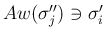 )。
)。
まず、(3) を
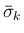 で書き直すと、
違いは膨張波とその分解 front の部分だけであり、
3.4 節で述べたように
膨張波の分解 front に対しては
で書き直すと、
違いは膨張波とその分解 front の部分だけであり、
3.4 節で述べたように
膨張波の分解 front に対しては 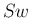 は共通なので、
は共通なので、
また、後 (3.10 節) で出てくるが、
解の存在定理では 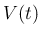 が十分小さい場合のみ
考えていて、よって各 front の大きさも十分小さく、
例えば Lemma 7.2 (i) の
が十分小さい場合のみ
考えていて、よって各 front の大きさも十分小さく、
例えば Lemma 7.2 (i) の 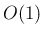 の部分も、定理で必要な評価ではすべて
の部分も、定理で必要な評価ではすべて
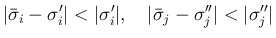
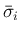 と
と 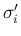 ,
および
,
および
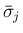 と
と 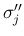 はそれぞれ同符号となり、
真性非線形の特性族では
衝撃 front かそうでないかが一致することになる。
よって、
はそれぞれ同符号となり、
真性非線形の特性族では
衝撃 front かそうでないかが一致することになる。
よって、
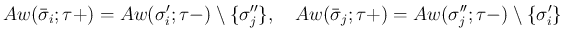
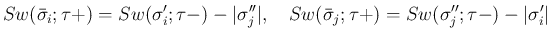
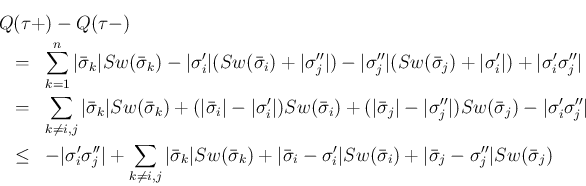
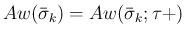 (
(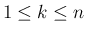 ) は、
) は、
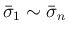 を含まず、
よって
を含まず、
よって 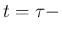 の front 全体に含まれてしまうので、
の front 全体に含まれてしまうので、
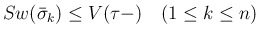
竹野茂治@新潟工科大学