3.4
 の評価: 記号
の評価: 記号
 の評価: 記号
の評価: 記号
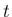 に対して、
に対して、
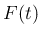 を時刻
を時刻 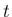 に存在する front 全体の集合、
に存在する front 全体の集合、
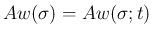 を、front
を、front 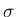 に approach する
に approach する 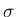 以外のすべての front (時刻
以外のすべての front (時刻 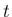 で存在するもの) の集合、
で存在するもの) の集合、
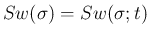 を、
を、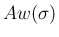 に属する front の大きさ
全体の和とする (いずれも
に属する front の大きさ
全体の和とする (いずれも 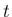 に依存)。
なお、
に依存)。
なお、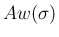 ,
, 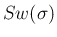 の
の 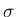 は、
front の大きさではなく、オブジェクトとしての front 自体を
意味し、(詳しくは 2.3 節参照)、
は、
front の大きさではなく、オブジェクトとしての front 自体を
意味し、(詳しくは 2.3 節参照)、
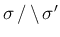 は
は 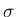 と
と 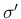 が approach することを
意味するものとする。
が approach することを
意味するものとする。
また、front に分解する前の膨張波 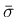 に対しても
に対しても
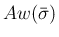 ,
,
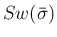 を用いることがあるが、
その意味は自明であろう。
を用いることがあるが、
その意味は自明であろう。
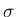 が膨張波
が膨張波 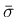 の分解 front の一つである場合、
明らかに
の分解 front の一つである場合、
明らかに
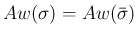 ,
,
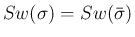 と
なる。
と
なる。
竹野茂治@新潟工科大学