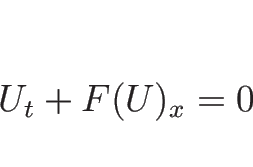4.1 はじめに

保存則方程式の代表的な例である理想気体の方程式では、 衝撃波という不連続な物理現象が存在するが、 この節ではそのような不連続な解について考察する。

もちろん、不連続な関数は微分できないので、その不連続なところでは 微分方程式

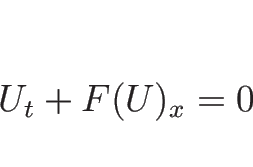$$U_t+F(U)_x=0$$ (4.50)

は満たされない。 もし、不連続な箇所が、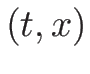$(t,x)$ 平面上のある曲線上であれば、 そこは全体では測度 0 の集合だから、といってそれを無視し、 その曲線以外では (4.1) を満足する関数を 解とすればいい、というわけではない。 それでは適切な衝撃波を再現できないし、解の一意性も保証できない。

では、その (4.1) に 「意味のある」不連続性とはどのようなものであるかを、 いくつかの角度から検討してみる。