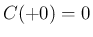
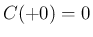 が導かれることを
説明する。
が導かれることを
説明する。
上の関数
が
で、
を満たし、かつ(30) は当然 (5) に対応するが、 「が非減少関数であれば、
が存在して
となる。
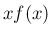 が非減少」というのは、
(4) の最後の条件から得られる (7) の
条件に対応する。よって命題 5 が成り立てば
が非減少」というのは、
(4) の最後の条件から得られる (7) の
条件に対応する。よって命題 5 が成り立てば 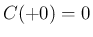 が
成り立つ。
が
成り立つ。
なお、この命題 5 は、
「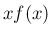 が非減少」という条件がなければ成り立たないことに注意する。
もし
が非減少」という条件がなければ成り立たないことに注意する。
もし 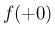 が存在すれば、(30) より
それが 0 でなければいけないことはすぐにわかるが、
が存在すれば、(30) より
それが 0 でなければいけないことはすぐにわかるが、
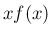 が非減少でなければ
が非減少でなければ 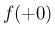 が存在しない例が容易に作れる。
例えば、
が存在しない例が容易に作れる。
例えば、
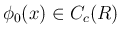 を
を
![\begin{displaymath}
\phi_0(x)\geq 0,
\hspace{1zw}\mathop{\mathrm{supp}}\phi_0\subset [1,2],
\hspace{1zw}\int\phi_0\, dx = 1
\end{displaymath}](img296.png)
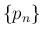 ,
, 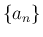 を
を
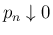 で
で
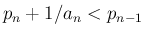 となるように取り、
となるように取り、
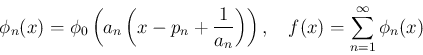
![$\mathop{\mathrm{supp}}\phi_n = [p_n,\ p_n+1/a_n]$](img302.png) は互いに交わらず、よって、
は互いに交わらず、よって、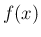 は
0 の近くで
は
0 の近くで  の幅で振動する関数となり、
もちろん
の幅で振動する関数となり、
もちろん 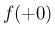 は存在しないが、
は存在しないが、
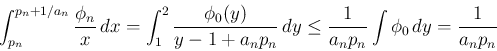
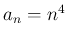 ,
, 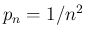 とすれば
とすれば
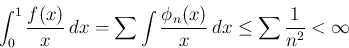
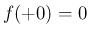 となるためには
となるためには 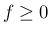 と (30) だけでは不十分であり、
「
と (30) だけでは不十分であり、
「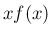 が非減少」のような条件が必要であることがわかる。
が非減少」のような条件が必要であることがわかる。
さて命題 5 を背理法で証明する。
もし、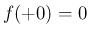 でないとすると、
でないとすると、
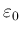 と数列
と数列 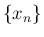 が存在する。
が存在する。
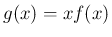 は増加関数なので、
は増加関数なので、
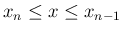 では、
では、
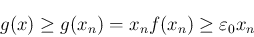
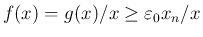 となり、
となり、
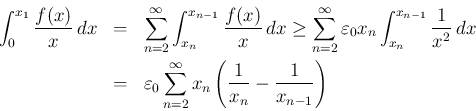
今、
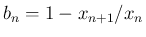 とすると、
とすると、
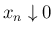 より
より 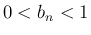 で、
(32) より
で、
(32) より
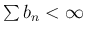 であるから
であるから 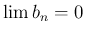 となり、
よって
となり、
よって 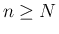 ならば
ならば 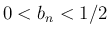 となるような
となるような 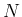 が存在する。
が存在する。
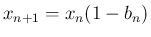 より、
より、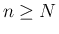 に対して
に対して
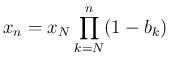 、
よって、
、
よって、
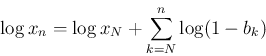
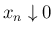 であったから、
が言えることになるが、
であったから、
が言えることになるが、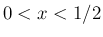 では
では
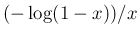 は
正でかつ有界な関数なので、
は
正でかつ有界な関数なので、
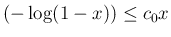 となる定数
となる定数 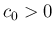 が取れる。
よって、
が取れる。
よって、
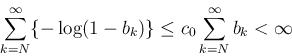
よって (31) となるような 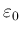 と
と 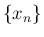 は
取れないことになり、命題 5 が成り立つことが示された。
は
取れないことになり、命題 5 が成り立つことが示された。
竹野茂治@新潟工科大学