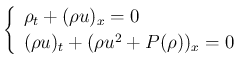 (1)
(1)
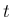 は時刻、
は時刻、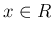 は位置、
は位置、
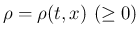 は気体の密度、
は気体の密度、
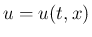 は気体の速度、
は気体の速度、
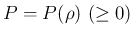 は気体の圧力を意味する。
は気体の圧力を意味する。
この方程式の Lax-Friedrichs 型差分近似解の有界性は、 通常微分方程式 (1) に対する Riemann 問題の 解の有界性と、 不変領域の凸性を用いて示されることが多いが、 それらを使わずに直接差分式から有界性を示す証明は、 ないわけではないだろうが、あまり見かけない。
その直接証明はかなりわずらわしいが不可能ではなく、 本稿ではそれを紹介する。
竹野茂治@新潟工科大学