����: 3.2 ������ʬ��������ʬ
���: 3 �٥����
����: 3 �٥����
(PDF �ե�����: series1.pdf)
3.1 ��«Ⱦ��
2.2 ��ε����ˤ�ꡢ
�Ȥʤ�褦�� 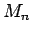 ��¸�ߤ���Ф��Υ٥�����ϡ�
���ξ�郎���������
��¸�ߤ���Ф��Υ٥�����ϡ�
���ξ�郎��������� 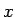 ���Ф������м�«���롣
���Τ褦�ʵ��
���Ф������м�«���롣
���Τ褦�ʵ��
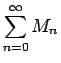 �Υ٥���� (8) ��ͥ��� �Ȥ�����
�Υ٥���� (8) ��ͥ��� �Ȥ�����
�����⤷
�Ǥ����硢
�Ǥ��뤫�顢�����١����Ƚ��ˡ�ˤ�� 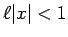 �����ʤ��
�����ʤ��
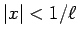 �ΤȤ��٥���� (8) �����м�«����
�ΤȤ��٥���� (8) �����м�«����
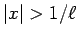 �ΤȤ���ȯ�����뤳�Ȥ��狼�롣
�Ĥޤꡢ0 ���濴�Ȥ��ơ�
�ΤȤ���ȯ�����뤳�Ȥ��狼�롣
�Ĥޤꡢ0 ���濴�Ȥ��ơ�
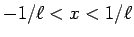 ���ϰϤǼ�«���뤳�Ȥˤʤ뤬��
���̤ˡ����Τ��Ȥ������롣
���ϰϤǼ�«���뤳�Ȥˤʤ뤬��
���̤ˡ����Τ��Ȥ������롣
���� 11
�ɤ�ʥ٥���� (8) ���Ф��Ƥ⡢
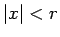 �ʤ�����м�«��
�ʤ�����м�«��
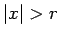 �ʤ��ȯ��
�ʤ��ȯ��
�Ȥʤ�褦��
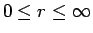 ��¸�ߤ��롣
��������
��¸�ߤ��롣
��������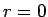 �ΤȤ��ϡ�
�ΤȤ��ϡ�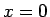 �ʳ��Ǥϼ�«���ʤ� (
�ʳ��Ǥϼ�«���ʤ� (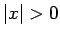 �ʤ��ȯ��)��
�ʤ��ȯ��)��
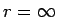 �ΤȤ��ϡ����٤Ƥ�
�ΤȤ��ϡ����٤Ƥ� 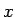 ���Ф��Ƽ�«���� (
���Ф��Ƽ�«���� (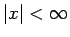 �ʤ�м�«)
���Ȥ��̣���롣
�ʤ�м�«)
���Ȥ��̣���롣
���� 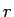 ���Υ٥������ ��«Ⱦ�� �ȸƤ֡�
���Υ٥������ ��«Ⱦ�� �ȸƤ֡�
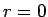 �Ǥ���褦�ʥ٥�����Ȥ��Ƥϡ��㤨��
�Ǥ���褦�ʥ٥�����Ȥ��Ƥϡ��㤨��
�����뤷��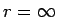 �Ǥ���褦�ʥ٥�����Ȥ��Ƥϡ��㤨��
�Ǥ���褦�ʥ٥�����Ȥ��Ƥϡ��㤨��
�����롣���Ԥ�
�Ȥʤ�Τǡ�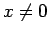 �ʤ�Ф��Υ٥�����ϼ�«���ʤ�����Ԥ�
�ʤ�Ф��Υ٥�����ϼ�«���ʤ�����Ԥ�
�Ȥʤ�Τǡ��ɤ�� 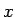 ���Ф��Ƥ����м�«���롣
���Ф��Ƥ����м�«���롣
��«Ⱦ�¤ϡ����̤˼��Τ褦�ʼ��Ǥ���蘆��뤳�Ȥ��Τ��Ƥ���:
���ΰ�̣��ޤ�ơ��ܤ������Ȥ˴ؤ��Ƥϡ����ϳؤξܤ����ܡ�
���뤤�ϵ�����˴ؤ�����ҤȤ��Ƥ�餤��������
����������Ƚ��ˡ�ȴ�Ϣ�����뤳�Ȥ��ܤ�������������Ȼפ���
�ºݡ�������κǽ�˾Ҳ𤷤��褦�ˡ�
�ʤ�� 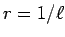 �Ȥʤ롣
�Ȥʤ롣
�ޥ��������Ÿ����ͭ�¹�ˤ�������⡢��«Ⱦ����Ǥ϶���ˤʤ뤬��
��«Ⱦ�³��Ǥ϶���ˤϤʤ�ʤ�����
��«Ⱦ����Ǥ��«Ⱦ�¤˶ᤤ 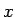 �ǤϤ��ζ�������٤ϰ����ʤ롣
�ǤϤ��ζ�������٤ϰ����ʤ롣
����: 3.2 ������ʬ��������ʬ
���: 3 �٥����
����: 3 �٥����
�����м������㹩�����
2006ǯ9��26��
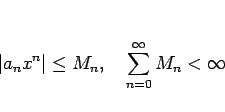
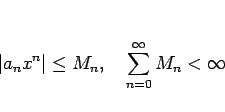
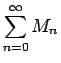 �Υ٥���� (8) ��ͥ��� �Ȥ�����
�Υ٥���� (8) ��ͥ��� �Ȥ�����
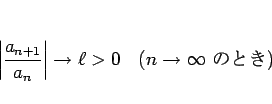
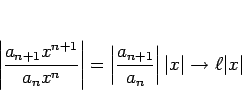
![]() ���Υ٥������ ��«Ⱦ�� �ȸƤ֡�
���Υ٥������ ��«Ⱦ�� �ȸƤ֡�
![]() �Ǥ���褦�ʥ٥�����Ȥ��Ƥϡ��㤨��
�Ǥ���褦�ʥ٥�����Ȥ��Ƥϡ��㤨��
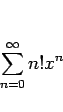
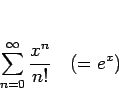
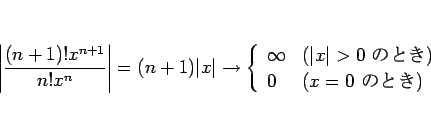
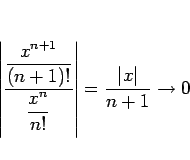
![\begin{displaymath}
r=\frac{1}{\displaystyle \limsup_{n\rightarrow\infty}\sqrt[n]{\vert a_n\vert}}
\end{displaymath}](img158.gif)
![\begin{displaymath}
\lim_{n\rightarrow\infty}\left\vert\frac{a_{n+1}}{a_n}\right...
...ޤ��� }
\lim_{n\rightarrow\infty}\sqrt[n]{\vert a_n\vert}=\ell
\end{displaymath}](img159.gif)
![]() �ǤϤ��ζ�������٤ϰ����ʤ롣
�ǤϤ��ζ�������٤ϰ����ʤ롣