7 数値計算
6 節の考察により、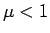 か
か 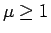 かで
かで 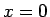 での境界条件 (6) の要、不要が分かれることがわかったが、
それを数値計算結果と比較してみることにする。
での境界条件 (6) の要、不要が分かれることがわかったが、
それを数値計算結果と比較してみることにする。
それは、(5) の数値計算を通常の差分で考えると、
その計算方法は 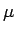 が 1 より大きいか小さいかとは
無関係に計算できてしまうからで、つまり差分の作り方によって
が 1 より大きいか小さいかとは
無関係に計算できてしまうからで、つまり差分の作り方によって
-
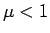 で、境界条件 (6) を必要とする計算方法の場合
で、境界条件 (6) を必要とする計算方法の場合
-
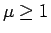 で、境界条件 (6) を必要とする計算方法の場合
で、境界条件 (6) を必要とする計算方法の場合
-
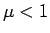 で、境界条件 (6) を使わない計算方法の場合
で、境界条件 (6) を使わない計算方法の場合
-
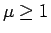 で、境界条件 (6) を使わない計算方法の場合
で、境界条件 (6) を使わない計算方法の場合
の 4 通りがあることになるが、
6 節の考察により 1. と 4. は正しく、
2. は無用な境界条件を与えていることになっていて、
逆に 3. は
必要な境界条件がない状態になっているはずである。
本節では、これらの計算方法を実際にどのように行うのか、
そしてその結果と 6 節の考察との関係について紹介する。
方程式 (5) を普通に差分化すると
のようなものが考えられるが、これだと 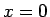 の近くで、
の近くで、
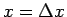 での
での 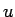 の値を計算するときに
の値を計算するときに 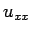 の差分の
の差分の 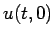 の値を用いるので
の値を用いるので 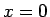 での境界条件が必要になってしまう。
これを解消するには、
での境界条件が必要になってしまう。
これを解消するには、
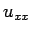 の差分の
の差分の
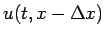 の項に、
の項に、
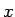 倍の代わりに
倍の代わりに 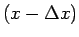 倍がついていればよく、
そうすれば
倍がついていればよく、
そうすれば 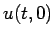 の計算のときはそれが 0 倍となって消えてくれることになる。
つまり、
の計算のときはそれが 0 倍となって消えてくれることになる。
つまり、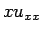 の差分の代わりに
の差分の代わりに 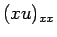 の差分を考えればよいことになる。
の差分を考えればよいことになる。
よって、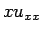 を
を
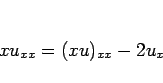
と変形して、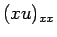 の差分を
の差分を
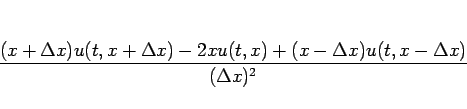 |
(30) |
とすればよい。
残る 1 階微分の 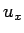 の項は、(29) では前進差分としているが、
その場合には
の項は、(29) では前進差分としているが、
その場合には 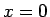 での境界条件は必要なく、
これを後退差分とすると
での境界条件は必要なく、
これを後退差分とすると 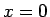 での境界条件が必要となる。
での境界条件が必要となる。
結局、方程式 (5) を、
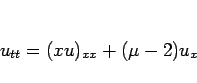
と書き直した上で、
2 階微分の項は 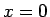 での境界条件が不要な形 (30) を利用することにして、
1 階微分は前進差分とした
での境界条件が不要な形 (30) を利用することにして、
1 階微分は前進差分とした
を 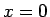 での境界条件が不要な差分 (4 通りのうちの 3. と 4.) とし、
での境界条件が不要な差分 (4 通りのうちの 3. と 4.) とし、
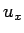 の差分を後退差分にした
の差分を後退差分にした
を 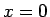 での境界条件が必要な差分 (4 通りのうちの 1. と 2.) として数値計算することにする。
での境界条件が必要な差分 (4 通りのうちの 1. と 2.) として数値計算することにする。
以下にその数値計算結果を示すが、いずれも 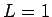 、初期値は
、初期値は
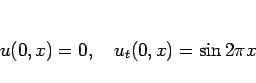
とし、境界条件が必要な差分では 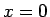 での境界条件は
での境界条件は
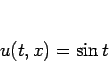
としている。
また、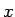 方向の分割数は
方向の分割数は 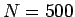 (
(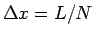 ) で、
) で、
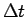 は
は
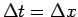 として計算した。
以下に示すグラフは、いずれも
として計算した。
以下に示すグラフは、いずれも 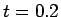 毎の
毎の 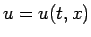 のグラフを
のグラフを
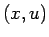 平面に約 50 本重ねて表示している。
平面に約 50 本重ねて表示している。
まずは、境界条件をつけた差分 (32) による結果を示す。
この差分では、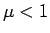 の場合は適切で、
の場合は適切で、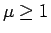 の場合は不適切、
すなわち境界条件が余計になっているはずである。
の場合は不適切、
すなわち境界条件が余計になっているはずである。
図 1 を見ると、
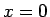 の付近では境界条件に引きずられて
糸が不自然に折れ曲がっているように見えなくもないが、
の付近では境界条件に引きずられて
糸が不自然に折れ曲がっているように見えなくもないが、
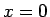 の付近を拡大した図 2 を見ると、
そうでもない感じがする。
の付近を拡大した図 2 を見ると、
そうでもない感じがする。
それに対して、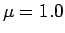 (図 3, 4),
(図 3, 4), 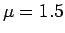 (図 5, 6) と
(図 5, 6) と 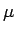 が大きくなるにつれ、
糸がかなり不自然に境界条件に引きずられ、
が大きくなるにつれ、
糸がかなり不自然に境界条件に引きずられ、
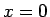 の近くで急に曲がっていることがわかる。
つまり、
の近くで急に曲がっていることがわかる。
つまり、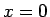 の付近では境界条件に拘束されて
不自然に急激に折れ曲がっていて、
それは本来は余計な境界条件のために
そのように不自然な形になっているのだと想像される。
の付近では境界条件に拘束されて
不自然に急激に折れ曲がっていて、
それは本来は余計な境界条件のために
そのように不自然な形になっているのだと想像される。
次は、境界条件の不要な差分 (31) による結果を示す。
この差分では、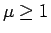 の場合が適切で、
の場合が適切で、
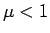 の場合は境界条件が足りないはずである。
の場合は境界条件が足りないはずである。
図 7, 8 は、
その 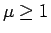 の場合のグラフであるが、
の場合のグラフであるが、
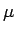 が大きい方が
が大きい方が 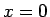 でのしなり (変動) が大きいと感じる (
でのしなり (変動) が大きいと感じる (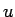 軸の目盛りに注意) が、特に問題は見られない。
軸の目盛りに注意) が、特に問題は見られない。
一方、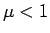 の場合は、
の場合は、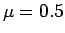 (図 9)、
(図 9)、
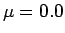 (図 10) も、
(図 10) も、
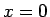 での振動が小さくなっているように感じるが、
それほど問題があるようには見えない。
での振動が小さくなっているように感じるが、
それほど問題があるようには見えない。
しかし、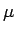 をさらに小さくして負の値にすると、
境界条件なしの差分 (31) では解の有界性が崩れて、
どんどん負の方に絶対値が大きくなっていく (図 11)。
これを、同じ
をさらに小さくして負の値にすると、
境界条件なしの差分 (31) では解の有界性が崩れて、
どんどん負の方に絶対値が大きくなっていく (図 11)。
これを、同じ 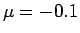 の値に対する境界条件つきの差分 (32) の結果 (図 12) と比較すると、
これもやや変わった感じのグラフではあるが、
安定性という点では境界条件つきの差分 (32) の方がましなように思う。
この不安定性は、本来必要な境界条件が足りないために起きているのであろうが、
この図 11 がそれを明確に表しているのかどうかは、
しかしよくはわからない。
の値に対する境界条件つきの差分 (32) の結果 (図 12) と比較すると、
これもやや変わった感じのグラフではあるが、
安定性という点では境界条件つきの差分 (32) の方がましなように思う。
この不安定性は、本来必要な境界条件が足りないために起きているのであろうが、
この図 11 がそれを明確に表しているのかどうかは、
しかしよくはわからない。
竹野茂治@新潟工科大学
2009年6月22日
![]() が 1 より大きいか小さいかとは
無関係に計算できてしまうからで、つまり差分の作り方によって
が 1 より大きいか小さいかとは
無関係に計算できてしまうからで、つまり差分の作り方によって
![]() を
を
![]() の項は、(29) では前進差分としているが、
その場合には
の項は、(29) では前進差分としているが、
その場合には ![]() での境界条件は必要なく、
これを後退差分とすると
での境界条件は必要なく、
これを後退差分とすると ![]() での境界条件が必要となる。
での境界条件が必要となる。
![]() 、初期値は
、初期値は
![]() の場合は適切で、
の場合は適切で、![]() の場合は不適切、
すなわち境界条件が余計になっているはずである。
の場合は不適切、
すなわち境界条件が余計になっているはずである。
![]() の付近では境界条件に引きずられて
糸が不自然に折れ曲がっているように見えなくもないが、
の付近では境界条件に引きずられて
糸が不自然に折れ曲がっているように見えなくもないが、
![]() の付近を拡大した図 2 を見ると、
そうでもない感じがする。
の付近を拡大した図 2 を見ると、
そうでもない感じがする。
![]() (図 3, 4),
(図 3, 4), ![]() (図 5, 6) と
(図 5, 6) と ![]() が大きくなるにつれ、
糸がかなり不自然に境界条件に引きずられ、
が大きくなるにつれ、
糸がかなり不自然に境界条件に引きずられ、
![]() の近くで急に曲がっていることがわかる。
つまり、
の近くで急に曲がっていることがわかる。
つまり、![]() の付近では境界条件に拘束されて
不自然に急激に折れ曲がっていて、
それは本来は余計な境界条件のために
そのように不自然な形になっているのだと想像される。
の付近では境界条件に拘束されて
不自然に急激に折れ曲がっていて、
それは本来は余計な境界条件のために
そのように不自然な形になっているのだと想像される。
![]() の場合が適切で、
の場合が適切で、
![]() の場合は境界条件が足りないはずである。
の場合は境界条件が足りないはずである。
![]() の場合は、
の場合は、![]() (図 9)、
(図 9)、
![]() (図 10) も、
(図 10) も、
![]() での振動が小さくなっているように感じるが、
それほど問題があるようには見えない。
での振動が小さくなっているように感じるが、
それほど問題があるようには見えない。