3 パラメータ変換による変形
本節では (1) の式を変形して、
それが 2 節で紹介した
内サイクロイドになるかどうかを考えてみる。
今、
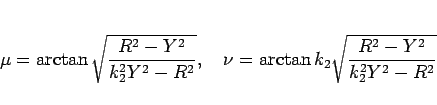 |
(10) |
とすると、(3) より
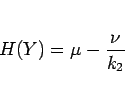 |
(11) |
となる。(10) より
であるから、
となるので、
となることがわかる。
(10) より
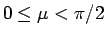 ,
,
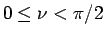 なので、
よって
なので、
よって
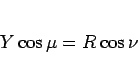 |
(12) |
が得られる。同様にして、
より
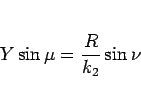 |
(13) |
が得られる。
さて、(12), (13) と
(1), (11) により、
となり、結局
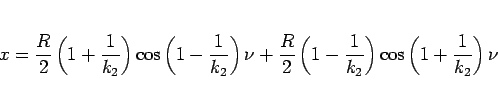 |
(14) |
が得られる。同様に 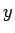 は、
は、
より、
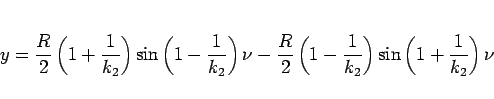 |
(15) |
と変形できる。
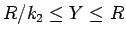 に対して
に対して
であり、よって
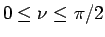 であるから、
であるから、
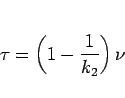 |
(16) |
とすると、その範囲は
となる。また、
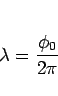 |
(17) |
とすると、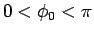 より
より 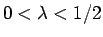 で、
で、
となるので、これらにより (14), (15) は
と書け、これは確かに (9) に一致する。
なお、これは (1) の
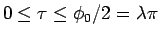 の
部分であるが、もう半分の
の
部分であるが、もう半分の
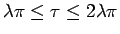 の方は、
(2) により、ここまでと全く同様にして得られる。
の方は、
(2) により、ここまでと全く同様にして得られる。
以上により、
均質な場合の地中最速降下線 (1), (2), (3) が、
確かに内サイクロイドに等しいことが確かめられたことになる。
そして、その小円の半径と大円の半径の比である 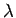 は、
(17) より出発点と終点とが作る中心角
は、
(17) より出発点と終点とが作る中心角 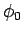 と、
と、
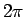 との比に等しいこともわかったことになる。
これは実際に 2 点が与えられたときに
内サイクロイドを用いて具体的な解を求めるのに役に立つだろう。
との比に等しいこともわかったことになる。
これは実際に 2 点が与えられたときに
内サイクロイドを用いて具体的な解を求めるのに役に立つだろう。
竹野茂治@新潟工科大学
2017年8月2日
![]() に対して
に対して
![]() の
部分であるが、もう半分の
の
部分であるが、もう半分の
![]() の方は、
(2) により、ここまでと全く同様にして得られる。
の方は、
(2) により、ここまでと全く同様にして得られる。
![]() は、
(17) より出発点と終点とが作る中心角
は、
(17) より出発点と終点とが作る中心角 ![]() と、
と、
![]() との比に等しいこともわかったことになる。
これは実際に 2 点が与えられたときに
内サイクロイドを用いて具体的な解を求めるのに役に立つだろう。
との比に等しいこともわかったことになる。
これは実際に 2 点が与えられたときに
内サイクロイドを用いて具体的な解を求めるのに役に立つだろう。