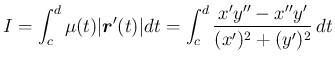 (14)
(14)
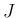 と書くことにする。
と書くことにする。
仮定 (4) より、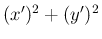 は常に正なので、
は常に正なので、
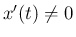 である
である 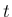 の範囲
の範囲 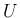 (
(![$[c,d]$](img109.png) の開部分集合) と、
の開部分集合) と、
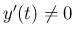 である
である 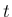 の範囲
の範囲 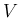 (
(![$[c,d]$](img109.png) の開部分集合) は
の開部分集合) は
![$U\cup V=[c,d]$](img112.png) となるが、
となるが、
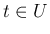 の範囲で (14) を積分すると、
の範囲で (14) を積分すると、
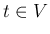 の範囲で積分すると、
の範囲で積分すると、
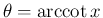 は値域は
は値域は 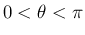 、
定義域は実数全体の減少関数で、
、
定義域は実数全体の減少関数で、
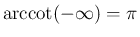 ,
,
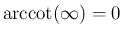 ,
,
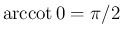 となる。
となる。
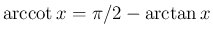 となることも容易にわかる。
となることも容易にわかる。
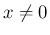 に対し、
に対し、
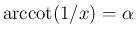 とすると、
とすると、
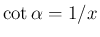 より
より 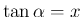 となるが、
となるが、
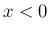 では
では
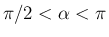 ,
, 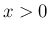 では
では
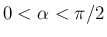 なので、
よって
なので、
よって
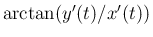 も
も
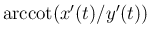 も
も 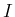 の滑らかな原始関数にはならない。
の滑らかな原始関数にはならない。
今、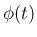 をベクトル
をベクトル
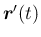 の偏角とする:
の偏角とする:
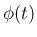 は
は 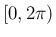 の範囲には制限せず、
の範囲には制限せず、
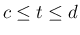 で滑らかに変化するように取り、
よって
で滑らかに変化するように取り、
よって 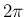 を越えたり負になったりしてもよいとする。
を越えたり負になったりしてもよいとする。
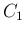 に交差はなく、また
に交差はなく、また 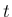 に伴なって
に伴なって
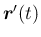 は
は 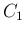 を
左回りに進むので、終点では
を
左回りに進むので、終点では
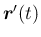 は始点より 1 回転反時計回りに回っていることになり (図 11)、
よって始点と終点の偏角の差は
は始点より 1 回転反時計回りに回っていることになり (図 11)、
よって始点と終点の偏角の差は
(18) より 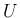 では
では
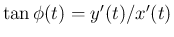 ,
,
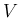 では
では
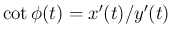 なので、
なので、
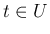 で
で
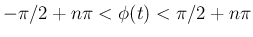 の範囲では
の範囲では
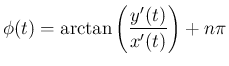
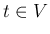 で
で
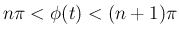 の範囲では
の範囲では
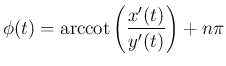
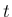 (
(
![$\in U\cup V=[c,d]$](img154.png) ) に対して
となり、よってこの偏角
) に対して
となり、よってこの偏角 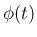 が (14) の
が (14) の 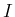 の
滑らかな原始関数であることがわかる。
よって、(19) より
の
滑らかな原始関数であることがわかる。
よって、(19) より
![$\displaystyle I = \left[\phi(t)\right]_c^d = \phi(d)-\phi(c) = 2\pi
$](img156.png)
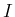 が求まり、結局 (13) の
が求まり、結局 (13) の 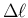 は
は 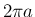 となること、
すなわち一般の閉曲線の場合でも
となること、
すなわち一般の閉曲線の場合でも 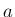 だけ離れた閉曲線との
弧長の差は
だけ離れた閉曲線との
弧長の差は 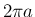 となることがわかった。
となることがわかった。
竹野茂治@新潟工科大学