![]() は、P
を通る緯線に接して東へ向くベクトルなので、
は、P
を通る緯線に接して東へ向くベクトルなので、
![]() をパラメータ t
で微分した導関数と同じ向きになる。
(1) より、
をパラメータ t
で微分した導関数と同じ向きになる。
(1) より、
となり、 -
= r(-
sin t +
cos t)cos
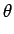
なので、よって、
| -sin t +
cos t| =
= 1
となる。 同様に、
= -
sin t +
cos t
(2)
で、
= r
cos
- r(
cos t +
sin t)sin
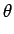
なので、
|cos
- (
cos t +
sin t)sin
| =
= 1
となる。
=
cos
-
sin
cos t -
sin
sin t
(3)
であり、 |
= r
sin
+ r(
cos t +
sin t)cos
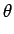
となる。なお、
=
sin
+
cos
cos t +
cos
sin t
(4)
| = | (- |
||
| = | - |
||
| - |
|||
| = | |||
| = |
竹野茂治@新潟工科大学