地球の自転に伴って、P はその点を通る緯線上を円運動する。
その緯線の円の中心を A とすると、A は地軸上にあり、
QP と
![]() のなす角は
のなす角は
![]() /2 -
/2 - ![]() であるから、
|
であるから、
|![]() | = r sin
| = r sin![]() なので
なので
となる (図 3)。
= (r sin
)
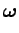
次に
![]() を表現するために、
このベクトルの乗る平面を表すベクトル、
すなわち自転軸に垂直な単位ベクトルを 2 つ取る。
それは
を表現するために、
このベクトルの乗る平面を表すベクトル、
すなわち自転軸に垂直な単位ベクトルを 2 つ取る。
それは
![]() = (0, sin
= (0, sin![]() , cos
, cos![]() )
に垂直なベクトルであるから、
ex
= (1, 0, 0)
と
)
に垂直なベクトルであるから、
ex
= (1, 0, 0)
と
を取ればよい。 なお、
=
x
= (0, sin
, cos
) x (1, 0, 0) = (0, cos
, - sin
)
この緯線の半径は
r cos![]() であり、
P はこの円周上を等速に進んでいくから、
であり、
P はこの円周上を等速に進んでいくから、
![]() はパラメータ t
を用いて
はパラメータ t
を用いて
と表される。これは、t の増加に伴って、 ex から
= r cos
(
cos t +
sin t)
これらにより、
![]() は、
は、
竹野茂治@新潟工科大学