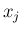
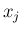 (
(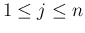 ) は正規分布に従うが、
それぞれの平均と分散は違っていてもよいとする。すなわち、
であるとするが、先にこれを標準化する。
となるので、これを使って
) は正規分布に従うが、
それぞれの平均と分散は違っていてもよいとする。すなわち、
であるとするが、先にこれを標準化する。
となるので、これを使って
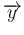 を表す。
(1) を行列化し、
とする。
一般に
を表す。
(1) を行列化し、
とする。
一般に 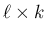 行列
行列 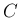 ,
, 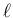 次元列ベクトル
次元列ベクトル
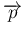 ,
, 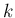 次元列ベクトル
次元列ベクトル
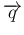
![$\displaystyle C = [c_{i,j}]_{\ell,k}
=\left[\begin{array}{c}\overrightarrow{\ha...
...\overrightarrow{q}=\left[\begin{array}{c}q_1\\ \vdots\\ q_k\end{array}\right],
$](img17.png)
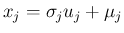 は
は
![$\displaystyle \overrightarrow{x}=\overrightarrow{u}\otimes\overrightarrow{\sigm...
...rightarrow{\mu}=\left[\begin{array}{c}\mu_1\\ \vdots\\ \mu_n\end{array}\right]
$](img20.png)
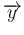 は
は
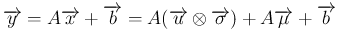
![\begin{eqnarray*}A(\overrightarrow{u}\otimes\overrightarrow{\sigma})
&=&
\left...
...ight]
\\ &=&
(A\oplus\overrightarrow{\sigma})\overrightarrow{u}\end{eqnarray*}](img23.png)
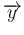 は
と
は
と
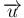 の一次式として表されることになる。
の一次式として表されることになる。
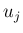 は
は 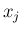 の一次式なので、
の一次式なので、
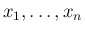 が独立なら
が独立なら
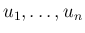 も (
も (
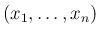 の
の 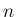 次元分布に関して) 独立で、
逆に
次元分布に関して) 独立で、
逆に
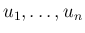 が独立なら、
が独立なら、
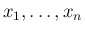 も (
も (
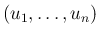 の
の 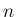 次元分布に関して) 独立となる ([1])。
よって、元の問題は、
次元分布に関して) 独立となる ([1])。
よって、元の問題は、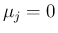 ,
, 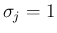 の
標準正規分布に関して独立性の判定ができれば、
一般の正規分布の場合でも (7) の形にしてから
標準正規分布に関して判定を行えばよいことになる。
よって、以後は
の
標準正規分布に関して独立性の判定ができれば、
一般の正規分布の場合でも (7) の形にしてから
標準正規分布に関して判定を行えばよいことになる。
よって、以後は 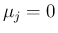 ,
, 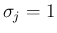 (
(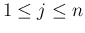 ) とする。
) とする。
一般に、連続確率変数
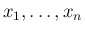 が独立であるとは、
が独立であるとは、
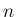 次元確率変数
次元確率変数
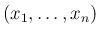 の
密度関数
の
密度関数
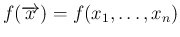 が、
各
が、
各 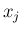 の密度関数
の密度関数 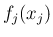 を用いて
を用いて
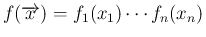
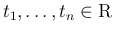 に対して、同時確率が
のように各
に対して、同時確率が
のように各 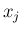 に対する確率の積で表される、と言い変えることもできる。
に対する確率の積で表される、と言い変えることもできる。
本稿では、上で見たように
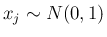 としてよいので、
としてよいので、
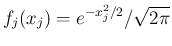 より、
より、
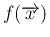 は
は
竹野茂治@新潟工科大学