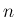
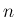 次元連続分布
次元連続分布
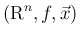 に対し、
に対し、
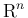 上の実数値関数
上の実数値関数
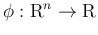 に対して
に対して
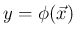 によって
連続確率変数
によって
連続確率変数 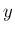 が決まるかを考える。
が決まるかを考える。
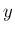 の分布関数
の分布関数 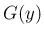 は、(24) より
は、(24) より
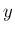 が連続分布となるためには、一点の確率
が連続分布となるためには、一点の確率
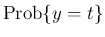 は 0、すなわち
は 0、すなわち
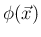 に対して成り立つわけではない。
例えば、
に対して成り立つわけではない。
例えば、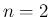 の場合に、ある面積を持った領域の上で
の場合に、ある面積を持った領域の上で 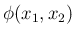 が
定数 (
が
定数 (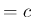 ) であれば、
) であれば、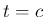 のとき (33) の
積分領域はその領域を含み、よって (33) の
積分値は正となりうる。
のとき (33) の
積分領域はその領域を含み、よって (33) の
積分値は正となりうる。
つまり、
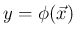 が連続確率変数となるためには、
すべての
が連続確率変数となるためには、
すべての
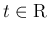 に対して (33) が
成り立つことが必要条件となる。
に対して (33) が
成り立つことが必要条件となる。
逆にそれを満たしていれば、(32) で定まる
分布関数 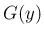 が条件 (16) を満たすことは、
連続性を除いては容易にわかり、
連続性についても積分論のやや難しい定理 (ルベーグ収束定理) と (33) から示すことができる。
これにより密度関数
が条件 (16) を満たすことは、
連続性を除いては容易にわかり、
連続性についても積分論のやや難しい定理 (ルベーグ収束定理) と (33) から示すことができる。
これにより密度関数 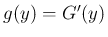 も決定し、
連続分布
も決定し、
連続分布
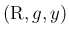 が確かに決定することになる。
が確かに決定することになる。
なお、より細かいことを言えば、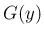 が連続というだけでは
その微分可能性は得られないが、
が連続というだけでは
その微分可能性は得られないが、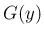 は単調なので、
「ほとんどの点で」微分可能であることが保証される。
は単調なので、
「ほとんどの点で」微分可能であることが保証される。
この場合も、離散分布の場合と同様に、平均の計算が 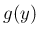 の代わりに
の代わりに
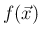 の方で計算できることを示す。
の方で計算できることを示す。
連続分布
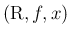 の平均は、
の平均は、
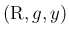 の平均は、
となるが、これが
の平均は、
となるが、これが 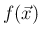 による計算
に一致することを、次の節で詳細に示すが、おおざっぱな「説明」を
以下に紹介する。
による計算
に一致することを、次の節で詳細に示すが、おおざっぱな「説明」を
以下に紹介する。
非常に小さい正数 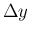 を取り、積分を
を取り、積分を
![$\displaystyle E[y]
= \int_{\mbox{\boldmath\scriptsize R}}yg(y)dy
= \sum_{j=-\infty}^{\infty}\int_{j\Delta y}^{(j+1)\Delta y}yg(y)dy
$](img127.png)
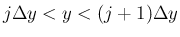 では
では
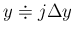 なので (32) より
なので (32) より
![\begin{eqnarray*}E[y]
&\doteqdot&
\sum_{j=-\infty}^{\infty}j\Delta y\int_{j\D...
... j\Delta y<\phi(\vec{x})\leq (j+1)\Delta y\}}
f(\vec{x})d\vec{x}\end{eqnarray*}](img130.png)
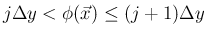 では
では
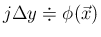 なので、
なので、
![$\displaystyle E[y]
\doteqdot \sum_{j=-\infty}^{\infty}
\int_{\{\vec{x}\vert j\D...
...\vec{x}
=\int_{\mbox{\boldmath\scriptsize R}^n}\phi(\vec{x})f(\vec{x})d\vec{x}
$](img133.png)
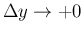 とすることで等号となる、
といった具合である。
とすることで等号となる、
といった具合である。
竹野茂治@新潟工科大学