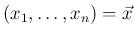
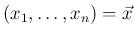 のようなベクトル表記も用いることにする。
のようなベクトル表記も用いることにする。
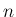 次元離散分布
次元離散分布
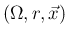 と、
と、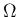 上の実数値関数
上の実数値関数
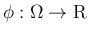 に対して、
に対して、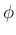 の像を
の像を
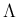 は有限集合か可算集合で、
は有限集合か可算集合で、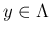 に対して
によって
に対して
によって
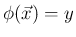 となる確率を与える関数を定めることができる。
ここで、和は
となる確率を与える関数を定めることができる。
ここで、和は
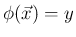 となるすべての
となるすべての 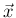 に対する
に対する 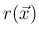 の和を意味する。
これにより、
の和を意味する。
これにより、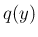 を確率関数とする確率変数
を確率関数とする確率変数
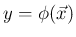 、
すなわち確率分布
、
すなわち確率分布 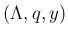 が定まる。
が定まる。
このようなやり方で、例えば 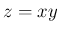 や
や
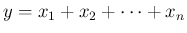 のような
複数の確率変数の式で表される確率変数が作られることになる。
のような
複数の確率変数の式で表される確率変数が作られることになる。
さて、離散確率分布 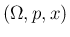 に対する平均
に対する平均 ![$E[x]$](img51.png) は、
は、
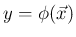 の、
この平均
の、
この平均 ![$E[y]$](img53.png) の計算について考える。
(9) より、
の計算について考える。
(9) より、
![$\displaystyle E[y]
= \sum_{y\in\Lambda} yq(y)
= \sum_{y\in\Lambda} y\sum_{\{\v...
...y\}} \phi(\vec{x})r(\vec{x})
= \sum_{\vec{x}\in\Omega} \phi(\vec{x})r(\vec{x})
$](img54.png)
![$E[y]$](img53.png) の計算を、
の計算を、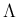 の代わりに
の代わりに 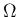 上の値で
のように計算できることになる。
この右辺を
上の値で
のように計算できることになる。
この右辺を
![$E[\phi(\vec{x})]$](img56.png) のように書く。
のように書く。
竹野茂治@新潟工科大学