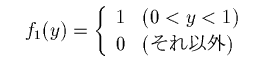
講義中に配布したプリントを、 画像ファイルと PDF ファイルにして置きます。 手書きなので多少 (かなり ?) 見にくいですが配布しているものと同じものです。
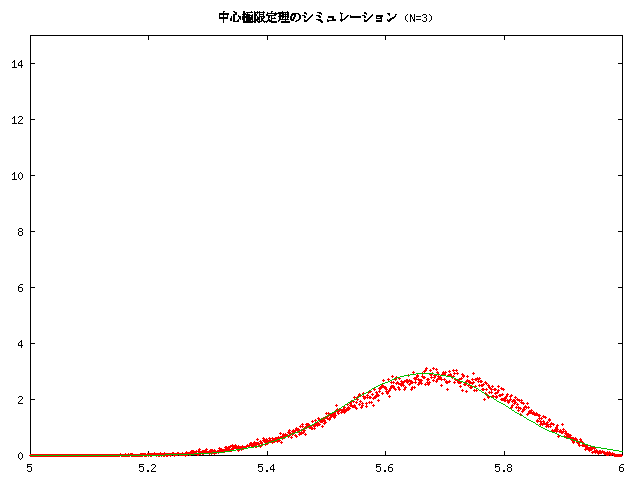
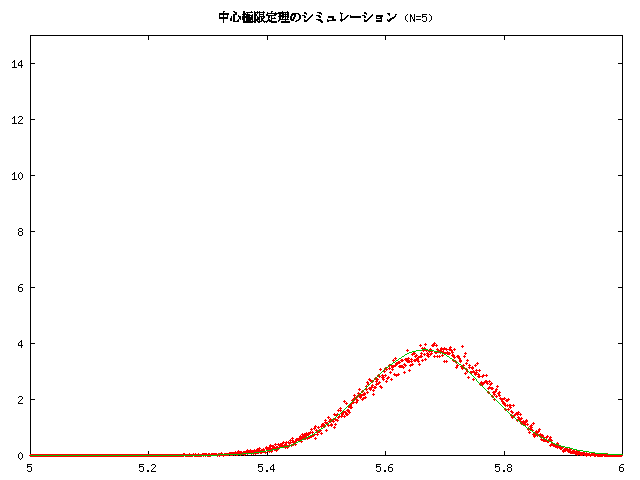
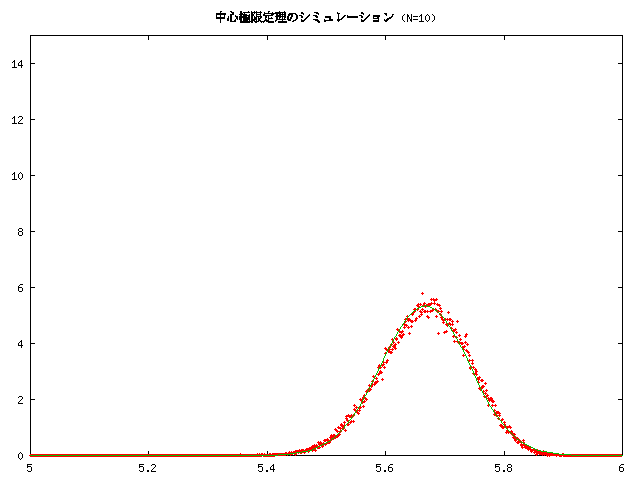
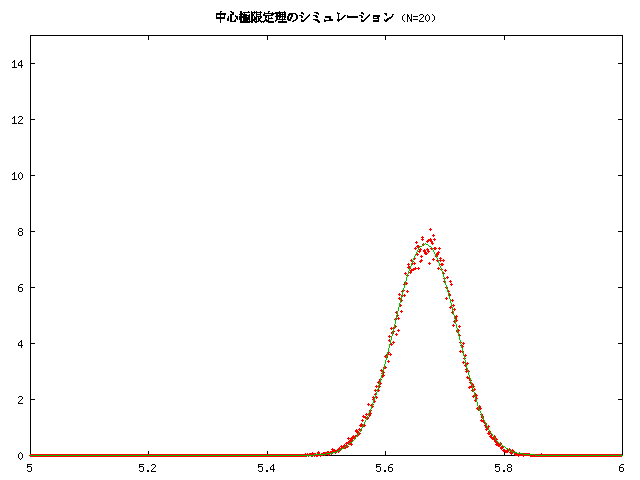
講義中にも紹介しましたが、 ある確率分布に従う独立同分布なたくさんの確率変数の平均は、 正規分布に近くなる、というものをシミュレーションしてみました。 ここではそれについて紹介しておきます。
ある確率分布に従う確率変数を生成するには、[0,1) を一様分布する 乱数を使います。 [0,1) を一様分布する乱数は、それ自身、次のような関数を密度関数とする 確率変数 (y) と見ることができます。
これを使って、任意の確率分布に従う確率変数を作ることができます。 それには、 "Numerical Recipes in C"(W.H.Press 他、丹慶勝市他訳、技術評論社) p215-216 にあるように、その確率分布の分布関数の逆関数を使って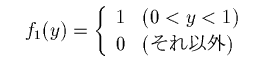
とすればいいだけです。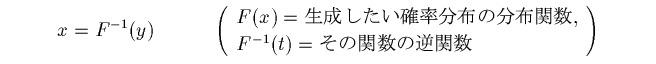
後は、それに従って、y の値をたくさん生成させて x の値の分布を 取ればいいだけなので、簡単にコンピュータでシミュレーションできます。
これは次のような平均、分散を持ちます。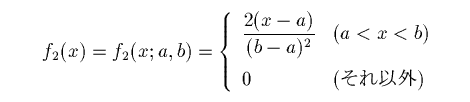
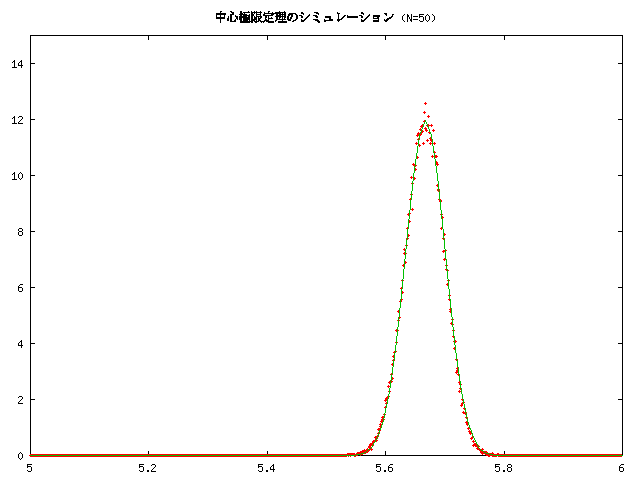
なお、実験では a=5.0, b=6.0 としています。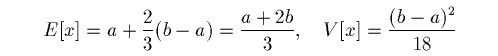
実線が元の密度関数のグラフです。だいたい一様乱数による度数分布は 密度関数と似た感じに分布しているように見えます。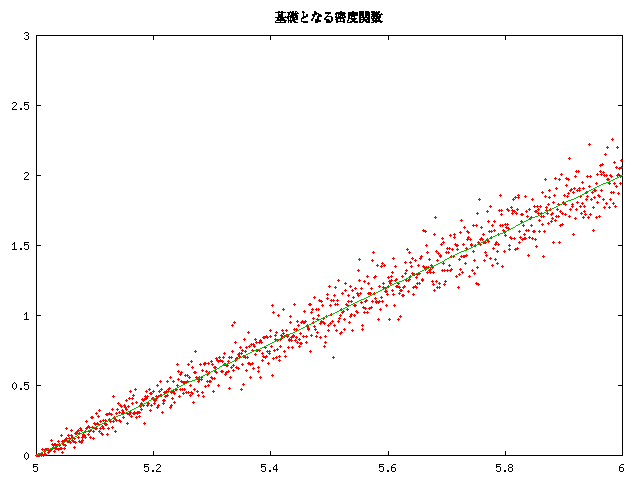
の密度関数のグラフです。中心極限定理は、元の分布が何であっても、 N が大きくなるとこの正規分布に近づいて行くという主張です。
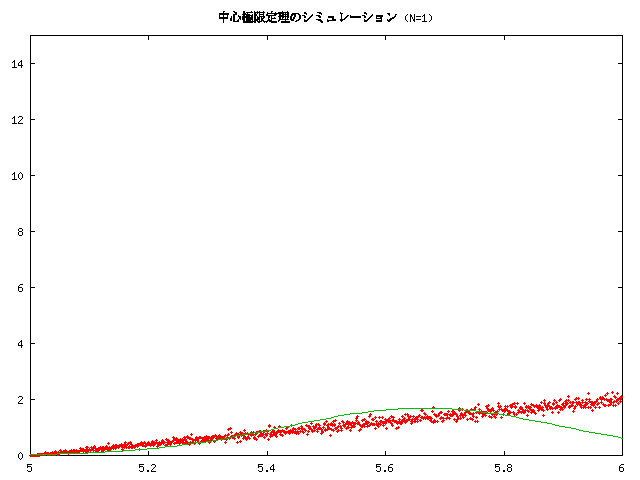
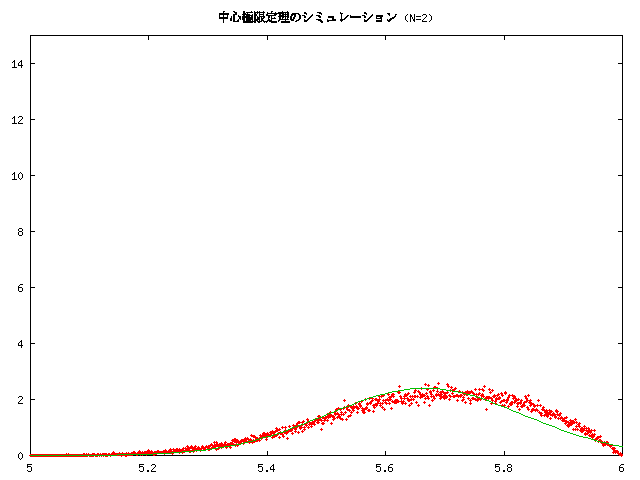
講義中にも紹介しましたが、 銀行窓口などの客と客との時間間隔のようなアクセス時間間隔は、 ある自然な仮定の元で指数分布になり、 一定時間内のアクセス回数はポアソン分布になります。
そこで、例えば WWW サーバへのアクセスやメールサーバへのアクセスも そのようになっているか、 うちの研究室のサーバのログを元に調べてみました。 これらのサーバにはアクセスログという履歴ファイルが残りますが、 そこからアクセス間の時間間隔を計測し、 適当な時間幅に対するヒストグラムを書いてみます。
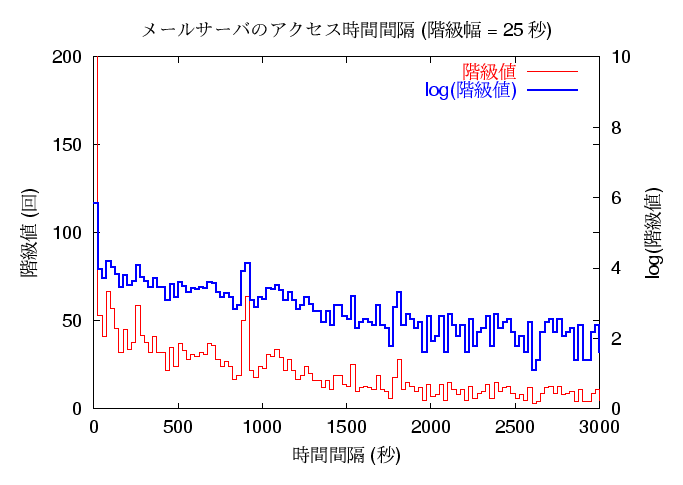
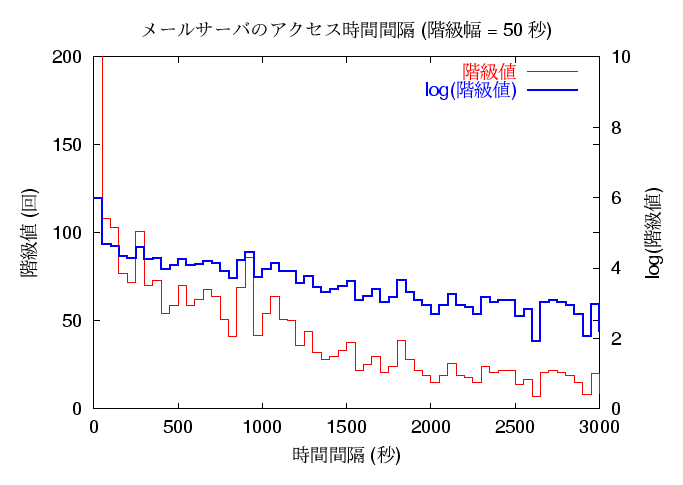
メールサーバの方は 03/22 ~ 05/23 までのもの (3333 件)、 WWW サーバの方は 02/19 ~ 05/23 までのもの (441610 件) を使用しました。 メールサーバの方はデータが多くないので、 あまり滑らかなグラフにはなりません。 しかも、変化の様子を細かくみるために度数分布の階級幅を短くすると、 ノイズの影響をまともに受けるので、階級幅をあまり短くもできません。 以下は、階級幅を 25 秒毎としたものと 50 秒毎としたもののヒストグラムを、 階級値をそのまま高さとしたものと、その対数を取って高さとしたグラフを 重ねて描いたものです。
次は WWW サーバですが、こちらはデータが多いので階級幅が小さくても かなり滑らかなグラフになります。 以下は、階級幅を 5 秒毎としたものと 10 秒毎としたもののグラフです。
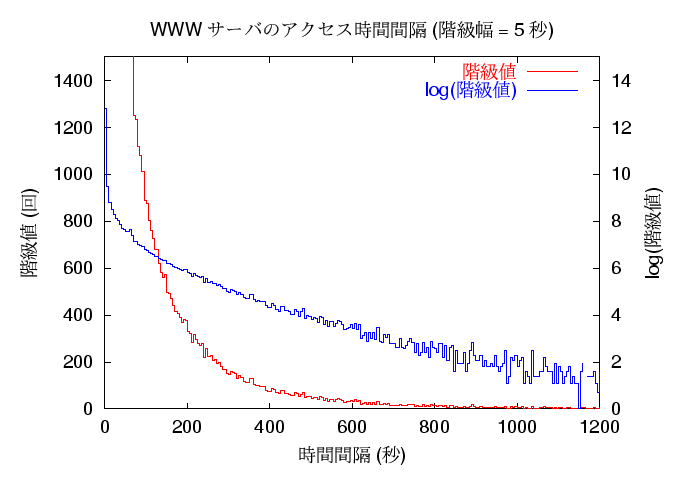
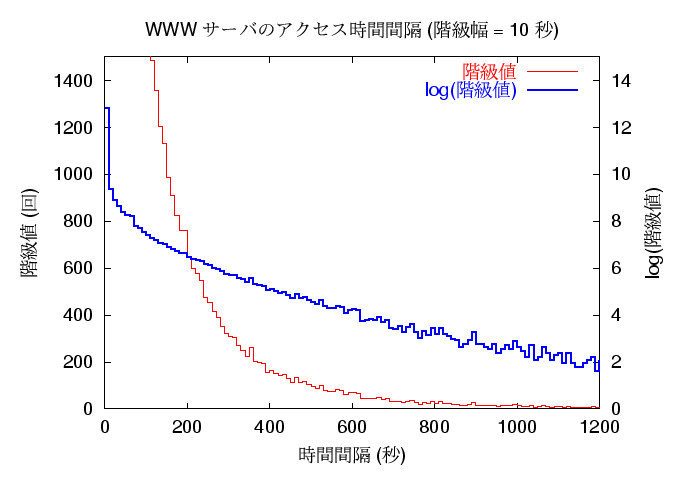
時間間隔が指数分布でない、ということは一定時間のアクセス数も ポアソン分布ではない、ということを意味していますので、 例えば負荷分散などの調査目的でインターネットのサーバアクセスの シミュレーションをアクセス回数がポアソン分布に従うとして行なう、 といったことを聞くことがありますが、 それは負荷が非常に高い状況ではあまり実際の状況を反映しない、 という風にも考えられるのではないでしょうか。
(06/13 2003)連続分布の場合、確率変数 x と y が独立であるということと、 (x,y) の密度関数が、x の密度関数と y の密度関数の積であること、 および (x,y) の分布関数が、x の分布関数と y の分布関数の積であること、 はいずれも同値になりますが、その証明はとばしましたのでここに載せます。
下のいずれかをどうぞ。
PDF ファイルを追加し、HTML 版にそれへのリンクを追加しました。
(01/13 2009)
超幾何分布の平均と分散、およびその極限が二項分布になることの計算は 面倒なので講義ではとばしました。ここに載せておきます。
下のいずれかをどうぞ。
PDF ファイルを追加し、HTML 版にそれへのリンクを追加しました。
(01/13 2009)
一般の連続分布に対する中心極限定理の証明は、かなり準備が必要で 難しいのですが、二項分布に関する中心極限定理 (ド・モアブル = ラプラスの定理) は、スターリングの定理を使えば ある程度の計算で証明できますのでそれをここに載せます。
下のいずれかをどうぞ。
PDF ファイルを追加し、HTML 版にそれへのリンクを追加しました。
(01/13 2009)
この講義の最初の年に、 相関係数と回帰直線に関するある疑問を感じて少し計算したのですが、 それをまとめましたので、ここに置きます。
HTML 版に PDF ファイルへのリンクを追加しました。
(01/13 2009)
「確率・統計」の講義の点推定のところで、 教科書などには不偏分散と標本分散は どちらも母分散の一致推定量である、と書いてあったのですが、 証明は省略されていたのが気になり、自分で計算してみました。 ここにそれをまとめておきます。
講義では 2 次元確率分布と、2 つの確率変数の独立性について紹介しましたが、 一般の n 次元確率分布、n 個の確率変数の独立性については 詳しくは説明しなかったので、補足としてここにまとめておきます。
なお、現代的な公理的確率論ではなく、 講義と同じ古典的確率論の範疇で考えます。
正規分布に従う独立な確率変数の一次式が正規分布に従う、 という定理の証明を講義では省略しましたが、 それをここに置きます。 それに必要な e-x2 の定積分が π1/2 となることの証明もついでに紹介します。
なお、統計や確率の専門的な書物では、 通常特性関数や積率母関数などを使って計算、証明をするようですが、 ここでは、計算は少し大変ですが、より原始的な方法で計算します。
また、現代的な公理的確率論ではなく、 講義と同じ古典的確率論の範疇で考えます。
講義では、自由度 n のカイ自乗分布 χ2(n) の密度関数を証明なしに紹介しましたが、 ここにその証明を置きます。
ついでにそれに必要なガンマ関数 Γ(p) の性質についても紹介します。
講義では、自由度 n の t 分布 t(n) の密度関数を証明なしに紹介しましたが、 ここにその証明を置きます。
講義では、 標本分散が自由度が一つ下がったカイ自乗分布に従う、 という話をしましたが、 その理由は、n=2,3 の例だけ示して後は詳しく説明しませんでした。
実は、そこで使われる、正規分布に従う独立な確率変数 x1,...,xn の一次式として 作られる確率変数 y1,...,xm がいつ独立であるかどうかを調べることは、 結果は難しくないのですが、その証明はかなり面倒です。
その (かなり泥臭い) 証明をここにまとめておきます。
講義では、 標本分散が自由度が一つ下がったカイ自乗分布に従う、 という話をしましたが、 その理由は、n=2,3 の例だけ示して後は詳しく説明しませんでした。 ここで一般の n に対する証明をあげておきます。
講義では、 ポアソン分布と指数分布が「表裏」の関係にあることを 簡単に説明し、証明らしきものも紹介しましたが、 証明を略した部分もありました。
その証明の補足もかねて、
正規母集団の母平均の検定、推定をするのに、t 分布が使われますが、 標本平均と平方和で表せるある式が自由度 (n-1) の t 分布に従う、ということからきています。
講義でその説明をした際に、標本平均から表される式と、 平方和から表される式の独立性から、と話したのですが、 その独立性自体の証明は省略しました。 証明を略した部分もありました。
ここにその証明を置きます。
以前 「中心極限定理」 で、 二項分布に関するド・モアブル＝ラプラスの 中心極限定理の各点収束性について説明をしました。
しかし、通常「ド・モアブル＝ラプラスの定理」は、各点収束性よりもむしろ その分布関数の収束性を指すことも多いようで、 ネットの情報や、数学辞典などにも見受けられます。 一方で、その分布関数の収束性の証明もネットなどにいくつかあるようですが、 残念ながらあまり厳密な証明 (と思えるもの) はないようで、 各点収束の結果をそのまま積分したものや、 有限区間での積分に関して証明して、 それで終わりとするものなどが多いようですが、 それらは極限の順序交換が行えることの保証を与えていないので 厳密な証明にはなっていないように思われます。
その分布関数の収束性としての ド・モアブル＝ラプラスの中心極限定理の厳密な証明を紹介したもの、 および 「中心極限定理」 でのややあいまいな点の修正を行ったものを以下に置きます。
