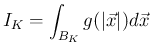 (3)
(3)
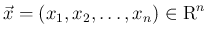 、
、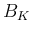 は原点中心で
半径が
は原点中心で
半径が 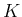 の
の 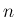 次元球
次元球
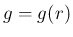 は
は 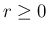 上の 1 変数関数である。
上の 1 変数関数である。
積分領域が球なので、通常は 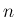 次元極座標
次元極座標
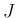 は
の形となる。よって、(3) は
となる。
は
の形となる。よって、(3) は
となる。
ここで、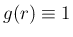 ならば (7) は
ならば (7) は 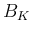 の
体積
の
体積 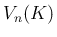 となるので、
となるので、
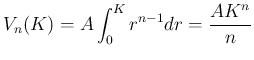
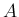 は
となる。
[1] で見たように、半径 1 の
は
となる。
[1] で見たように、半径 1 の 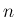 次元球の体積
次元球の体積 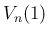 は
以下の式で表される。
ここで
は
以下の式で表される。
ここで 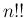 は
は 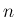 から 2 ずつ減らして 1, または 2 までかけたもの
である。
から 2 ずつ減らして 1, または 2 までかけたもの
である。
竹野茂治@新潟工科大学