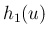
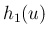 の存在性はかなり面倒な不等式の連続
であることがわかると思うが、
解析学分野ではこのような作業はよくあることであり、
そしてこのような不等式の積み重ねにより等号の成立を証明するのも
標準的な手法である。
の存在性はかなり面倒な不等式の連続
であることがわかると思うが、
解析学分野ではこのような作業はよくあることであり、
そしてこのような不等式の積み重ねにより等号の成立を証明するのも
標準的な手法である。
ただし、6 節の評価は、実は私にとってもそんなに易しい
ものではなく、
実際 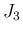 に関する評価は、7,8 回失敗した上でようやく
得たもので、
に関する評価は、7,8 回失敗した上でようやく
得たもので、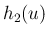 がきれいな形ではなく、
つぎはぎのようになっているのはそのためである。
しかし、これも解析学分野ではよくあることである。
がきれいな形ではなく、
つぎはぎのようになっているのはそのためである。
しかし、これも解析学分野ではよくあることである。
ちなみに、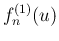 でなく、
でなく、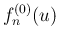 に対する
に対する 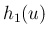 が
取れればもっと話は早いのであるが、
6 節の評価は
が
取れればもっと話は早いのであるが、
6 節の評価は
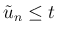 という上限を
実質的に使っているため
という上限を
実質的に使っているため 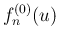 に対する
に対する 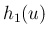 が
作れたことにはなっておらず、
それを作るのはもう一段難しい問題になる。
そして、
が
作れたことにはなっておらず、
それを作るのはもう一段難しい問題になる。
そして、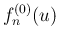 にそのようなものが実際に作れるかどうかは、
今のところは私にはわからない。
にそのようなものが実際に作れるかどうかは、
今のところは私にはわからない。
竹野茂治@新潟工科大学