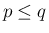
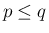 の場合、すなわち
の場合、すなわち 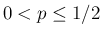 の場合
のみ証明すれば良いことを先に示しておく。
なおその場合、厳密に言えば、(3) だけでなく、
等号を除いたバージョン
も必要になる。
の場合
のみ証明すれば良いことを先に示しておく。
なおその場合、厳密に言えば、(3) だけでなく、
等号を除いたバージョン
も必要になる。
もし、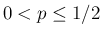 の場合に
(3), (9) が成り立てば、
の場合に
(3), (9) が成り立てば、
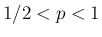 の場合は、
の場合は、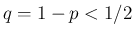 なので、
なので、
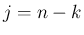 とすれば
とすれば
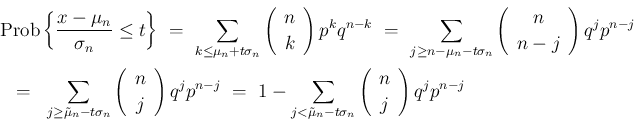
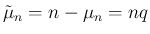 とした。
ここから
とした。
ここから
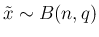 とすると、
とすると、
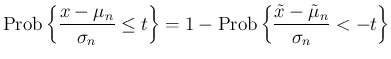
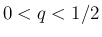 なので、(9) により
その極限は
なので、(9) により
その極限は
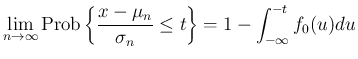
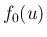 は偶関数なので、
は偶関数なので、
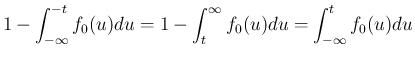
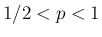 の場合にも (3) が
成り立つことになる。
の場合にも (3) が
成り立つことになる。
よって、以後は 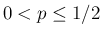 として任意の
として任意の 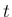 に対して (3), (9) が成り立つことを示す。
に対して (3), (9) が成り立つことを示す。
竹野茂治@新潟工科大学