(1)
とする。
(2)
とおくと、
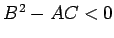 のとき、
のとき、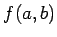 は極値であり、
は極値であり、
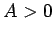 ならば極小、
ならば極小、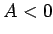 ならば極大である。
ならば極大である。
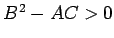 のとき、
のとき、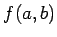 は極値でない。
は極値でない。
この定理の証明は、この教科書 [1] もそうだが、 2 変数関数のテイラー展開と、2 次形式の評価によるものが多い。 しかし、その方法は、微小評価や 2 次形式に不慣れな学生には 不向きではないかと思う。
本稿では、方向微分を用いることで、 1 変数関数の場合の極の判別法を応用した、 定理 38.2 の別の証明法を紹介することにする。
1 変数関数の場合の極の判別法として、 この教科書 [1] には、凸性を利用した次の定理が紹介されている。
この定理 17.4 では、![]() の場合に極かどうかの判定ができないものの、
通常の、増減表を書いて
の場合に極かどうかの判定ができないものの、
通常の、増減表を書いて ![]() の
の ![]() 以外での符号を調べる方法に比べ、
以外での符号を調べる方法に比べ、
![]() での
での ![]() ,
, ![]() の符号を見るだけで良いという点で優れている。
の符号を見るだけで良いという点で優れている。
2 変数の極の判別では、増減表を 2 次元的に書くことはできないので、 定理 38.2 は、むしろこの定理 17.4 に近く、 停留点での 2 階微分係数の符号を利用したものなのであるが、 本稿では、その定理 17.4 をより積極的に利用した証明を提示する。
竹野茂治@新潟工科大学