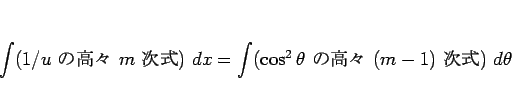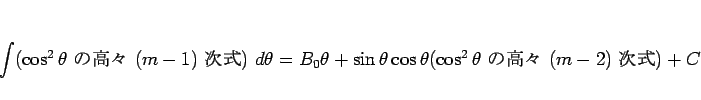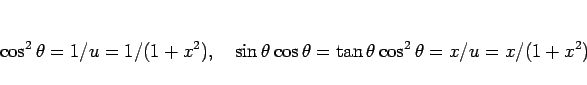次へ: 4 積分の計算例
上へ: '有理関数の積分について (その 2)'
前へ: 2 奇数次と偶数次の分離について
(PDF ファイル: quotef2.pdf)
3 積分の実行
2 節の計算により、
となる。
なお、これらの積分の中の 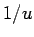 の高々
の高々 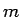 次式には定数項は含まれない。
次式には定数項は含まれない。
最初の 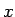 を一つ含む方は、
を一つ含む方は、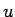 への置換積分により (
への置換積分により (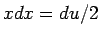 )
容易に
)
容易に
のように積分できる。
後者の方は、[1] で述べた方法では、
個々の積分に対しどうしても漸化式が必要になるので、
個々の積分ごとに見てもあまり楽にはならない。
よって、[1] の最後でも触れたように、
最終形を想定した未定係数法を用いるのが楽だと思う。
最終形は、[1] を見ればわかるが、
となる。なお、この最後の式の 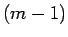 次式にも定数項は含まれない。
次式にも定数項は含まれない。
また、これには 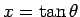 と置換してから
未定係数法を用いる、という方法もある。
この場合
と置換してから
未定係数法を用いる、という方法もある。
この場合
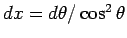 ,
,
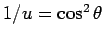 なので、
定数項がないことから
なので、
定数項がないことから
となり (この最後の式の 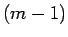 次式には定数項がありうる)、最終形は
次式には定数項がありうる)、最終形は
となる。これを 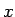 の式に戻すときは、
の式に戻すときは、
のようにすればいい。
次へ: 4 積分の計算例
上へ: '有理関数の積分について (その 2)'
前へ: 2 奇数次と偶数次の分離について
竹野茂治@新潟工科大学
2006年6月2日


![]() を一つ含む方は、
を一つ含む方は、![]() への置換積分により (
への置換積分により (![]() )
容易に
)
容易に
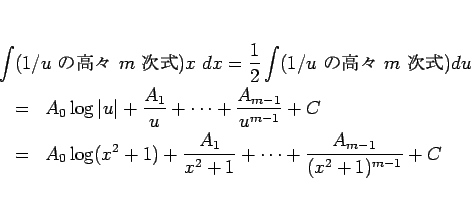
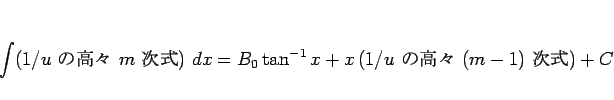
![]() と置換してから
未定係数法を用いる、という方法もある。
この場合
と置換してから
未定係数法を用いる、という方法もある。
この場合
![]() ,
,
![]() なので、
定数項がないことから
なので、
定数項がないことから