2 偏微分を用いた説明
まず、
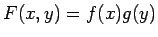 (
(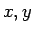 の 2 変数関数) とすると、
の 2 変数関数) とすると、
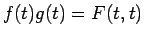 であり、よって
であり、よって
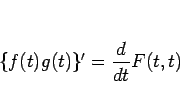 |
(3) |
となるが、2 変数関数の合成関数の微分法則
より、
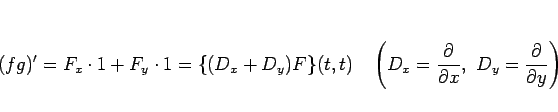 |
(5) |
となる。今、
とすると、(5) より
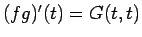 なので、
再び (5) と同じ計算を行えば、
なので、
再び (5) と同じ計算を行えば、
となる。ただし、この右辺は、
を意味することとする。
この計算を繰り返せば、
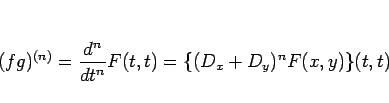 |
(6) |
となることがわかる。
そして、偏微分の順序交換の定理
を用いれば、
のような展開ができること、すなわち一般に
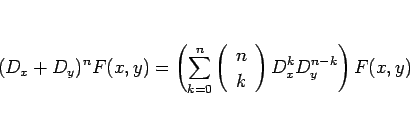 |
(7) |
となることが言える。
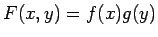 より、(7) の右辺は、
より、(7) の右辺は、
となるので、
結局 (6), (7), (8) より (1) が成り立つことがわかる。
竹野茂治@新潟工科大学
2006年12月27日
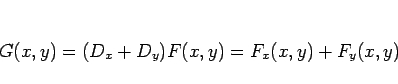
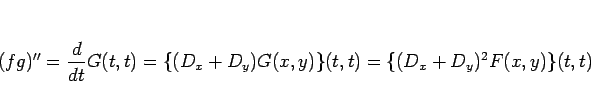
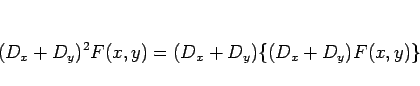
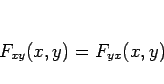
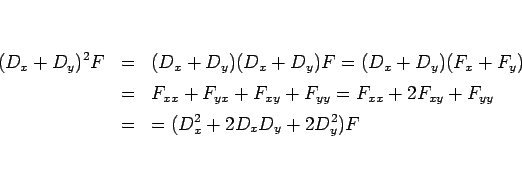
![]() より、(7) の右辺は、
より、(7) の右辺は、