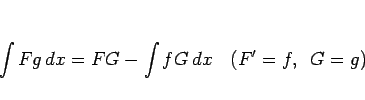
公式 2 は、公式 1 の「関数と導関数の関係」を、 一つ「原始関数と関数の関係」に書き直したものと見ることができる。 それをもう一方にも行えば、微分のない部分積分の公式を作ることができる。 それは以下の形となる。
微分が公式に入らないことでいいところもあるように見えるかもしれないが、
実際には、微分を表す ![]() の記号に対して、
原始関数を表す記号が
の記号に対して、
原始関数を表す記号が
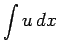 しかないため、
残念ながらこの公式 4 はあまり有用ではない。
例えば
しかないため、
残念ながらこの公式 4 はあまり有用ではない。
例えば ![]() の積分で考えてみると、
の積分で考えてみると、![]() は
は ![]() の積分なので、
の積分なので、
今、仮に ![]() の原始関数を
の原始関数を
![]() と書くことにすると、
公式 4 は、
と書くことにすると、
公式 4 は、
しかし、これは通常の部分積分の公式 1 とほぼ同等であり、 楽になっているわけではないし、独自の記号を用いる点、 あるいは原始関数の積分定数の不定部分の処理などの点で不利だと思われる。
竹野茂治@新潟工科大学