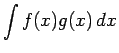 の一方を積分した
の一方を積分した
(10)
と置いてこの両辺を微分する:
を計算して、その結果を (10) に代入する
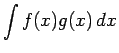 の一方を積分した
の一方を積分した
(10)
例として、
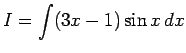 を計算してみる。
を計算してみる。
![]() の方のみを積分して、その余りを
の方のみを積分して、その余りを ![]() と置くと、
と置くと、
(11)
この方法 3 の長所は、
等だろう。これらの点では公式 1 や公式 2 よりも優れていると言えるが、逆に欠点は、積の微分は苦手な学生も多いので、 短所 1 は大きな欠点かもしれないが、 そのような学生には、例えば公式 1 の 長所 1 も長所にはならないので、 その点では公式 1 とは差し引きされるかもしれない。
また、短所 2 の「手間がかかる」という欠点も、 むしろ手間をかけて丁寧にやれば間違いが少ないということであり、 途中の計算も残りやすいので、そういう点ではよいことも多い。
しかし、最後の 短所 4 は、
例えば公式 1 であれば
「![]() よりも
よりも ![]() の積分の方が楽になる場合に部分積分は有効である」
と説明できるが、方法 3 ではそうはいかない、
ということを意味していて、これはある意味致命的で、
その有効性を認識してもらうためには公式 1 や公式 2 を示す必要があり、
方法 3 は補助的な使用に留まらざるを得ないと思う。
の積分の方が楽になる場合に部分積分は有効である」
と説明できるが、方法 3 ではそうはいかない、
ということを意味していて、これはある意味致命的で、
その有効性を認識してもらうためには公式 1 や公式 2 を示す必要があり、
方法 3 は補助的な使用に留まらざるを得ないと思う。
竹野茂治@新潟工科大学