4 証明その 1
まずは典型的な
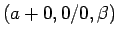 の場合の証明を紹介する。
の場合の証明を紹介する。
この場合に限らず、いずれの場合も証明には基本的に
「コーシーの平均値の定理」を用いる。
それをまず説明する。
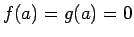 より、
より、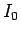 は
は
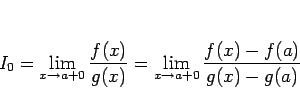
であるが、もし 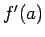 、
、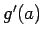 があって
があって 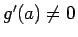 であれば、
であれば、
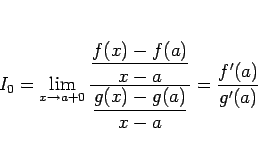
となるので、さらに 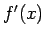 ,
, 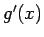 が
が 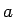 で連続であれば
この最後の値は
で連続であれば
この最後の値は 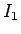 に等しいことになり、
ロピタルの定理が成立することになる。
ただし、この論法では元のロピタルの定理より強い仮定を
いくつか使ってしまっている (が、シンプルな証明の一つと言えるし、
実例ではこれで十分な場合も多い)。
に等しいことになり、
ロピタルの定理が成立することになる。
ただし、この論法では元のロピタルの定理より強い仮定を
いくつか使ってしまっている (が、シンプルな証明の一つと言えるし、
実例ではこれで十分な場合も多い)。
元の条件の下で証明するために、通常の平均値の定理を使うと、
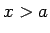 に対して、
に対して、
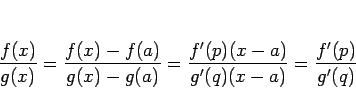
となるような 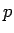 ,
, 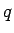 (
(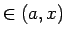 ) が取れる。
この式で
) が取れる。
この式で 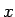 を
を 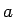 に近づけると
に近づけると 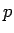 ,
, 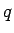 は
は 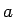 に近づくので
最後の項は
に近づくので
最後の項は 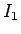 に近づきそうだが、
に近づきそうだが、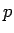 と
と 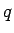 が揃っていないので、
その極限が
が揃っていないので、
その極限が 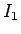 に等しいことの保証にはならない。
この
に等しいことの保証にはならない。
この 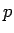 ,
, 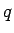 を同じ値に揃えることができる、
というのがコーシーの平均値の定理である。
を同じ値に揃えることができる、
というのがコーシーの平均値の定理である。
定理 2
(コーシーの平均値の定理)
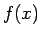 ,
, 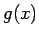 が
が ![$[a,b]$](img68.gif) で連続、
で連続、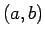 で微分可能で、
かつ
で微分可能で、
かつ 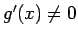 であるとき、
であるとき、
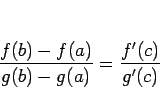
となる 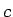 が
が 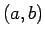 内に少なくとも一つ存在する。
内に少なくとも一つ存在する。
この定理の証明は、
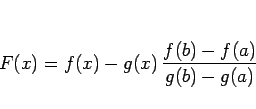
に対して通常の平均値の定理を使えば得られる。
なお、コーシーの平均値の定理の条件にある「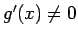 」は
外すことができない。例えば、
」は
外すことができない。例えば、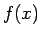 ,
, 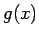 が、
が、
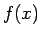 は
は 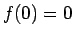 ,
, 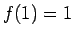 ,
, 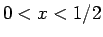 では増加、
では増加、
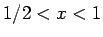 では減少、
では減少、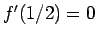 (例えば、
(例えば、
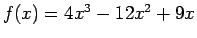 )
)
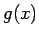 は
は 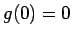 ,
, 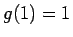 ,
, 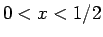 では減少、
では減少、
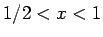 では増加、
では増加、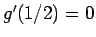 (例えば、
(例えば、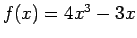 )
)
のような関数であれば、
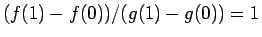 であるが、
であるが、
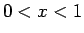 では、
では、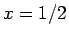 以外では
以外では 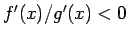 であり 1 に等しくなることはない。
であり 1 に等しくなることはない。
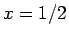 では
では 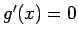 となるので、
これがコーシーの平均値の定理の条件を満たさない。
これが、ロピタルの定理 1 の
条件 2 に含まれる「
となるので、
これがコーシーの平均値の定理の条件を満たさない。
これが、ロピタルの定理 1 の
条件 2 に含まれる「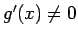 」の由来になる。
」の由来になる。
このコーシーの平均値の定理を用いて、
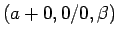 の場合の
ロピタルの定理の証明を、
の場合の
ロピタルの定理の証明を、
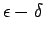 論法で行う。
論法で行う。
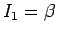 より、任意の
より、任意の 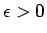 に対して、
に対して、
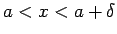 であるすべての
であるすべての 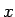 に対して、
に対して、
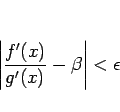 |
(2) |
となるような 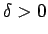 が取れる。
が取れる。
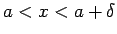 となる任意の
となる任意の 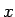 に対して、
コーシーの平均値を用いると、
に対して、
コーシーの平均値を用いると、
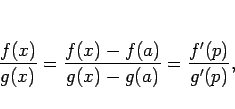
で
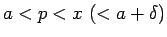 となる
となる 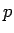 が存在する。
よって、(2) より
が存在する。
よって、(2) より
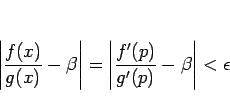
となる。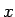 は
は 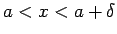 の任意の
の任意の 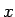 で、
で、
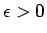 も任意なので、
これは
も任意なので、
これは 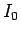 が存在して
が存在して 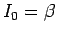 であることを示している。
これで、
であることを示している。
これで、
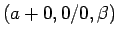 の場合の証明が終わった。
の場合の証明が終わった。
この証明は、
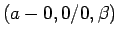 の場合もほぼ同じであるし、
その 2 つを合わせれば
の場合もほぼ同じであるし、
その 2 つを合わせれば 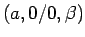 の場合になるので、
これも同様に示されることになる。
これで、
の場合になるので、
これも同様に示されることになる。
これで、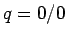 ,
, 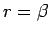 の場合のうち 3 通りのものの証明が終わる。
の場合のうち 3 通りのものの証明が終わる。
竹野茂治@新潟工科大学
2015年7月20日
![]() より、
より、![]() は
は
![]() に対して、
に対して、
![]() ,
, ![]() が
が ![]() で連続、
で連続、![]() で微分可能で、
かつ
で微分可能で、
かつ ![]() であるとき、
であるとき、
![]() 」は
外すことができない。例えば、
」は
外すことができない。例えば、![]() ,
, ![]() が、
が、
![]() の場合の
ロピタルの定理の証明を、
の場合の
ロピタルの定理の証明を、
![]() 論法で行う。
論法で行う。
![]() より、任意の
より、任意の ![]() に対して、
に対して、
![]() であるすべての
であるすべての ![]() に対して、
に対して、
![]() となる任意の
となる任意の ![]() に対して、
コーシーの平均値を用いると、
に対して、
コーシーの平均値を用いると、
![]() の場合もほぼ同じであるし、
その 2 つを合わせれば
の場合もほぼ同じであるし、
その 2 つを合わせれば ![]() の場合になるので、
これも同様に示されることになる。
これで、
の場合になるので、
これも同様に示されることになる。
これで、![]() ,
, ![]() の場合のうち 3 通りのものの証明が終わる。
の場合のうち 3 通りのものの証明が終わる。