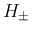
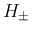 に関する以下の基本的な性質を示す。
に関する以下の基本的な性質を示す。
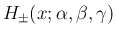 は、その両辺が積分の収束条件を
満たしていれば、以下の性質 [i]
は、その両辺が積分の収束条件を
満たしていれば、以下の性質 [i]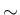 [v] が成り立つ。
[v] が成り立つ。
![$\displaystyle \begin{array}{cl}
\mathrm{[i]} &
\displaystyle \frac{d}{dx}H_{\...
...+1,\gamma+1)
\\
& \ +\beta H_{\pm}(x;\alpha+1,\beta,\gamma+1)=0
\end{array}$](img37.png)
[i]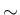 [iv] はほぼ自明で、[v] は部分積分で容易に示される。
[iv] はほぼ自明で、[v] は部分積分で容易に示される。
定理 1 から、
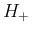 と
と 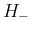 で共通の性質が成り立つことがわかる。
で共通の性質が成り立つことがわかる。
気体の方程式に対する証明では、1 節で伸べたように 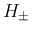 を何回か微分する必要があるが、
性質 [i] より、微分するとその分
を何回か微分する必要があるが、
性質 [i] より、微分するとその分 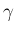 が下がる。
が下がる。
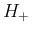 は
は 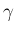 が小さくてもそのまま積分で表現できるのだが、
が小さくてもそのまま積分で表現できるのだが、
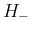 の方は
の方は 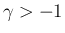 という制限があり、
その先の微分は、性質 [i] がそのままは使えない。
それは、別な式で表すことは可能なのだが、少し項が増えてしまい、
それを繰り返すと複雑な式になってしまう (例えば [4])。
それを防いで、同じ [i] のままの形で表現するために、
次節で
という制限があり、
その先の微分は、性質 [i] がそのままは使えない。
それは、別な式で表すことは可能なのだが、少し項が増えてしまい、
それを繰り返すと複雑な式になってしまう (例えば [4])。
それを防いで、同じ [i] のままの形で表現するために、
次節で 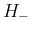 の
の 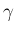 を
を 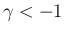 に対して拡張することを考える。
に対して拡張することを考える。
竹野茂治@新潟工科大学