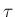
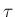 が整数である場合の従来の方法 [3] の一つの
簡略化を示した。
ここで、
が整数である場合の従来の方法 [3] の一つの
簡略化を示した。
ここで、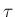 は、気体の断熱定数
は、気体の断熱定数 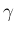 (
(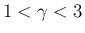 ) に
対して、
によって決まる正の定数。
) に
対して、
によって決まる正の定数。
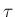 が非整数の場合は、Darboux の公式によってあたえられる
一般化エントロピーの分数階微分の計算、評価によって、
補償コンパクト性理論により [4],[5],[6] 等で
弱解の存在証明が得られているが、
が非整数の場合は、Darboux の公式によってあたえられる
一般化エントロピーの分数階微分の計算、評価によって、
補償コンパクト性理論により [4],[5],[6] 等で
弱解の存在証明が得られているが、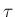 が整数の場合に対して
それは格段に難しく複雑である。
が整数の場合に対して
それは格段に難しく複雑である。
その一般化エントロピーは、
以下のような関数 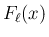 を用いて構成される。
を用いて構成される。
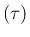 は
は 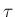 の小数部分を意味する。
の小数部分を意味する。
[2] を 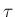 が非整数な場合に拡張、
すなわち [4],[5],[6] の証明の簡略化を行うには、
が非整数な場合に拡張、
すなわち [4],[5],[6] の証明の簡略化を行うには、
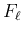 の
の ![$[\tau]+2$](img15.png) 階までの導関数、
およその
階までの導関数、
およその
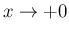 ,
,
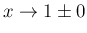 ,
,
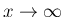 の
極限とその収束 order の評価が必要になる。
の
極限とその収束 order の評価が必要になる。
本稿では、(2) を少し一般化した以下の関数を考える。
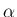 ,
, 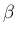 ,
, 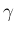 はいずれも整数ではないとする。
(3), (4) の条件を満たす
はいずれも整数ではないとする。
(3), (4) の条件を満たす 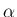 ,
, 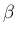 ,
, 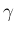 についてはこれらの積分は収束し、
についてはこれらの積分は収束し、
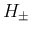 により (2) の
により (2) の 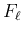 は
は
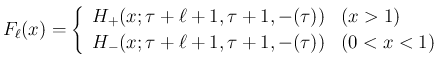
この
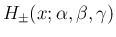 は変数変換により、
いわゆる超幾何関数 (hyper geometric function)
は変数変換により、
いわゆる超幾何関数 (hyper geometric function)
よって本稿では、超幾何関数に関する既知の結果を用いず、
(3), (4) の形の 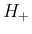 ,
, 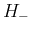 のままで
[2] の拡張のために必要となる性質や、
境界への極限とその収束 order などを考察する。
のままで
[2] の拡張のために必要となる性質や、
境界への極限とその収束 order などを考察する。
竹野茂治@新潟工科大学