

Next: 4 問題の図形が直円錐の一部になる条件
Up: 斜円錐の側面積について
Previous: 2 問題
(PDF ファイル: yokoyama1.pdf)
3 問題の定式化
この節で問題の設定を明確にしておく。
2 節の最後に述べたように、
元の問題を少し一般化して考えることにする。
まず、3 次元空間を考え、中心が原点である 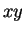 平面上の
以下の楕円を底面とする。
平面上の
以下の楕円を底面とする。
そして頂点 P の座標を
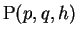 (
(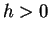 ) とする (図 6)。
元々の問題は、
) とする (図 6)。
元々の問題は、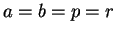 ,
, 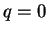 の場合に相当することになる。
の場合に相当することになる。
底面の楕円周上の点は
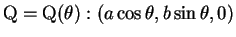 (
(
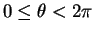 ) とパラメータ表示される
(注:
) とパラメータ表示される
(注: 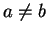 の場合には
の場合には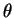 は一般には中心角とは異なる)。
よって、PQ を
は一般には中心角とは異なる)。
よって、PQ を 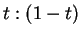 (
(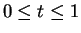 ) に内分する点を R とすれば
R の座標は
) に内分する点を R とすれば
R の座標は
となり、すなわちこの側面が 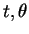 で以下のように
パラメータ表示されたことになる。
で以下のように
パラメータ表示されたことになる。
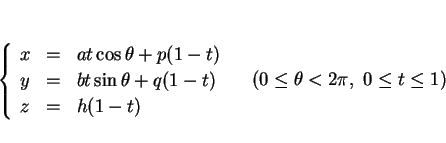 |
(2) |
この 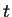 と
と 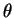 を消去すれば、
を消去すれば、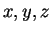 のみによる曲面の表示式も得られる。
のみによる曲面の表示式も得られる。
より、
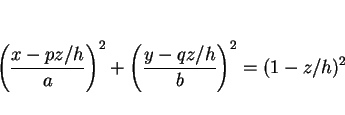 |
(3) |
となる。この式を 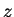 について解いて
について解いて 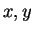 の式で表せば、
領域
の式で表せば、
領域 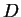 上の曲面
上の曲面 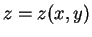 に対する曲面積の公式
に対する曲面積の公式
によって側面積を表すことができる。
しかし式 (3) を 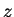 について解くのは、
2 次方程式なので一応可能ではあるが少し面倒だし、
そもそもその後の積分の計算が大変になりそうなので、
むしろパラメータ表示 (2) に対する面積分公式
を用いた方が良い。
について解くのは、
2 次方程式なので一応可能ではあるが少し面倒だし、
そもそもその後の積分の計算が大変になりそうなので、
むしろパラメータ表示 (2) に対する面積分公式
を用いた方が良い。
なお、この (3) から、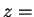 (定数) とした式、
すなわちこの曲面の水平断面の形は、どの高さでも底面の楕円と相似な楕円
(ただし中心はずれている) になっていることがわかる。
元の問題の場合には常に円になっていることになるので、
それを利用したような計算法はないかとも考えたのだが
それは見出せなかった。
(定数) とした式、
すなわちこの曲面の水平断面の形は、どの高さでも底面の楕円と相似な楕円
(ただし中心はずれている) になっていることがわかる。
元の問題の場合には常に円になっていることになるので、
それを利用したような計算法はないかとも考えたのだが
それは見出せなかった。


Next: 4 問題の図形が直円錐の一部になる条件
Up: 斜円錐の側面積について
Previous: 2 問題
Shigeharu TAKENO
2005年 2月 28日
![]() 平面上の
以下の楕円を底面とする。
平面上の
以下の楕円を底面とする。
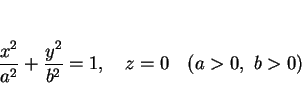
![]() (
(
![]() ) とパラメータ表示される
(注:
) とパラメータ表示される
(注: ![]() の場合には
の場合には![]() は一般には中心角とは異なる)。
よって、PQ を
は一般には中心角とは異なる)。
よって、PQ を ![]() (
(![]() ) に内分する点を R とすれば
R の座標は
) に内分する点を R とすれば
R の座標は
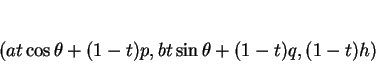
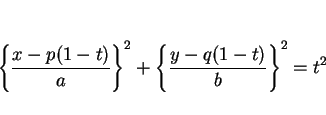
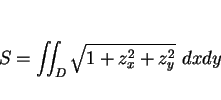
![]() (定数) とした式、
すなわちこの曲面の水平断面の形は、どの高さでも底面の楕円と相似な楕円
(ただし中心はずれている) になっていることがわかる。
元の問題の場合には常に円になっていることになるので、
それを利用したような計算法はないかとも考えたのだが
それは見出せなかった。
(定数) とした式、
すなわちこの曲面の水平断面の形は、どの高さでも底面の楕円と相似な楕円
(ただし中心はずれている) になっていることがわかる。
元の問題の場合には常に円になっていることになるので、
それを利用したような計算法はないかとも考えたのだが
それは見出せなかった。