6 大小の考察
以上により、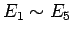 はすべて
はすべて 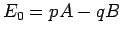 によって、
によって、
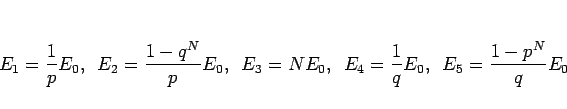
と表されることがわかった。
よって、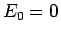 の場合は
の場合は 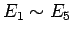 はすべて 0 となることになる。
はすべて 0 となることになる。
さて、通常のくじでは、あたりの確率 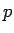 はかなり小さく (
はかなり小さく (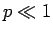 )、
代わりにあたりの賞金
)、
代わりにあたりの賞金 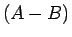 が参加料
が参加料 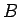 に比べて大きい (
に比べて大きい (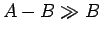 )。
そして、くじの主催者が損をしないように
)。
そして、くじの主催者が損をしないように 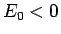 と設定されているだろう。
この条件の元で
と設定されているだろう。
この条件の元で 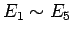 の大小を考えてみることにする。
の大小を考えてみることにする。
そのために、各 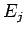 の
の 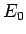 の係数を
の係数を 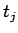 とし、
その
とし、
その 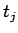 を比較することにする (
を比較することにする (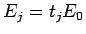 )。
)。
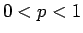 ,
, 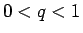 より明らかに
より明らかに
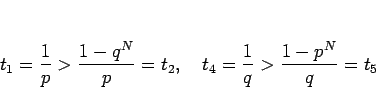
であり、また 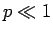 より
より
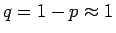 であるので、
であるので、
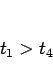
となる。また、
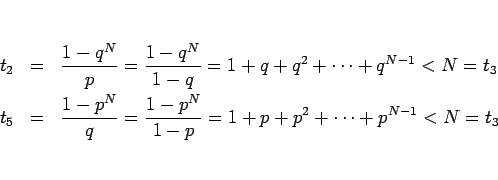
も言える。
次に 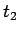 と
と 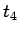 を比較してみる。
を比較してみる。
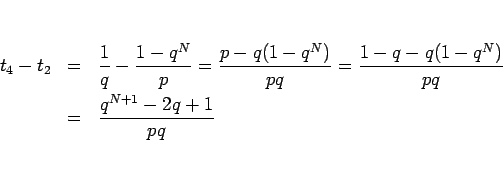
となるので、
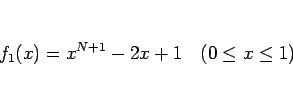
として、この 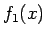 の符号を考える。
の符号を考える。
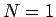 ならば、
ならば、
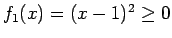 となる。
となる。
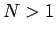 のときは、
のときは、
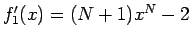 より、
より、
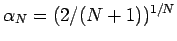 (
(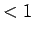 ) で
) で
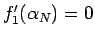 となり、
となり、
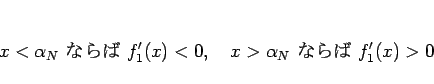
なので、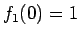 ,
, 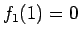 より、
より、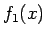 のグラフは
図 1 のようになる。
のグラフは
図 1 のようになる。
図 1:
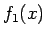 のグラフ
のグラフ
|
|
よって、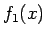 は零点
は零点 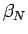 で符号が分かれ、
で符号が分かれ、
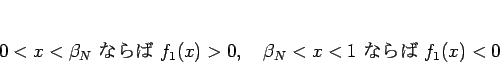
となる。
次に、この 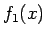 の零点である
の零点である 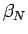 の大きさについて考えてみる。
の大きさについて考えてみる。
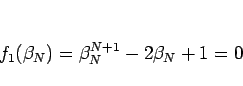
より、
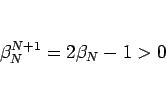
なので、まず 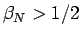 であることがわかる。
であることがわかる。
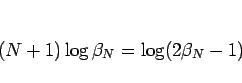
より、
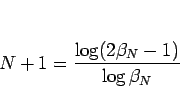
となるので、次に関数
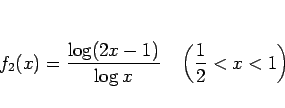
を調べてみる。ロピタルの定理より、
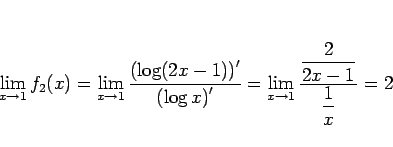
であり、
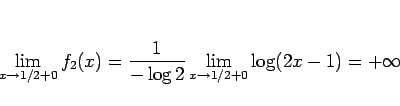
となっている。導関数は、
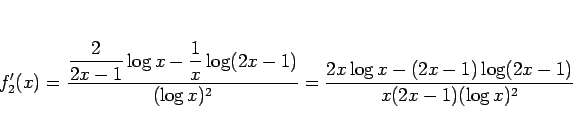
となるが、この分母は 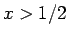 で正なので、分子を
で正なので、分子を 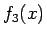 とすると、
とすると、
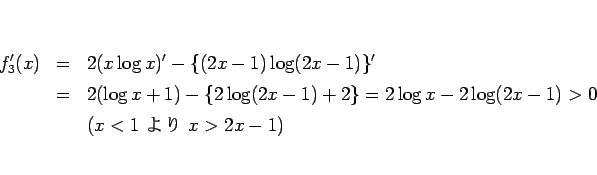
であり、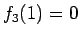 なので、
なので、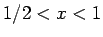 で
で 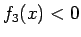 となる。
となる。
よって、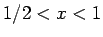 で
で 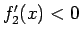 であり、
であり、
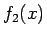 のグラフは図 2 のようになる。
のグラフは図 2 のようになる。
図 2:
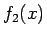 のグラフ
のグラフ
|
|
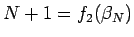 であるから、
よって
であるから、
よって 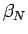 は
は 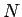 に関して単調に減少し、
に関して単調に減少し、
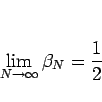
となること、
そして
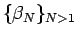 で一番大きいのは
で一番大きいのは 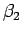 であることもわかる。
次に、この
であることもわかる。
次に、この 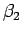 を求めてみる。
を求めてみる。
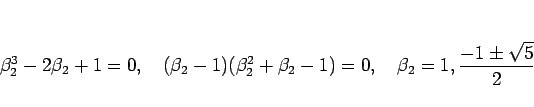
なので、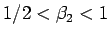 より
より
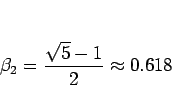
となる。
よって
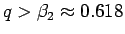 であれば、
すべての
であれば、
すべての 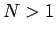 に対して
に対して 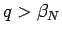 となるので
となるので 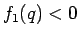 であり、
であり、
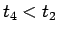 となる。
となる。
結局、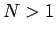 のときは、
のときは、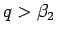 であれば、
であれば、
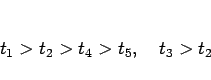
となる。ここで、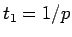 と
と 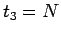 は独立な値なので、
は独立な値なので、
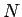 を変えることでその大小は変わりうる。
を変えることでその大小は変わりうる。
また、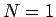 のときは、
のときは、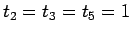 なので、
なので、
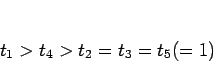
となる。
結局、今回の仮定の元 (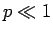 ,
, 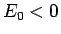 ) では、
) では、
であることになり、これらの中で一番損をしないのは 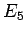 、
すなわち「はずれるまでやり、
、
すなわち「はずれるまでやり、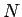 回でやめる」であることがわかる。
そして、
回でやめる」であることがわかる。
そして、
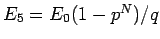 は
は 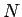 に関して単調減少であるから、
に関して単調減少であるから、
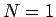 のときが最も大きい、すなわち 1 回だけやってやめる
(
のときが最も大きい、すなわち 1 回だけやってやめる
(
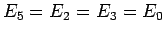 ) のが最も損をしない、ということになる。
) のが最も損をしない、ということになる。
竹野茂治@新潟工科大学
2007年4月28日
![]() はかなり小さく (
はかなり小さく (![]() )、
代わりにあたりの賞金
)、
代わりにあたりの賞金 ![]() が参加料
が参加料 ![]() に比べて大きい (
に比べて大きい (![]() )。
そして、くじの主催者が損をしないように
)。
そして、くじの主催者が損をしないように ![]() と設定されているだろう。
この条件の元で
と設定されているだろう。
この条件の元で ![]() の大小を考えてみることにする。
の大小を考えてみることにする。
![]() の
の ![]() の係数を
の係数を ![]() とし、
その
とし、
その ![]() を比較することにする (
を比較することにする (![]() )。
)。
![]() ,
, ![]() より明らかに
より明らかに
![]() と
と ![]() を比較してみる。
を比較してみる。
![]() ならば、
ならば、
![]() となる。
となる。
![]() のときは、
のときは、
![]() より、
より、
![]() (
(![]() ) で
) で
![]() となり、
となり、
![]() の零点である
の零点である ![]() の大きさについて考えてみる。
の大きさについて考えてみる。
![]() で
で ![]() であり、
であり、
![]() のグラフは図 2 のようになる。
のグラフは図 2 のようになる。
![]() であるから、
よって
であるから、
よって ![]() は
は ![]() に関して単調に減少し、
に関して単調に減少し、
![]() のときは、
のときは、![]() であれば、
であれば、
![]() のときは、
のときは、![]() なので、
なので、
![]() ,
, ![]() ) では、
) では、