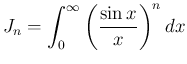 (1)
(1)
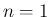 のものは、
ルベーグ積分では積分できないが、リーマン広義積分が存在する例として
有名なもので、ディリクレ積分とも呼ばれ、
その値は
のものは、
ルベーグ積分では積分できないが、リーマン広義積分が存在する例として
有名なもので、ディリクレ積分とも呼ばれ、
その値は 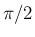 になることが知られている。
になることが知られている。
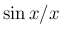 は、信号処理分野などでよく用いられるものらしく、
sinc 関数などという名前でも呼ばれている。
そのためか、意外に多くのサイトで (1) の計算が
紹介されているのに少し驚いた。
は、信号処理分野などでよく用いられるものらしく、
sinc 関数などという名前でも呼ばれている。
そのためか、意外に多くのサイトで (1) の計算が
紹介されているのに少し驚いた。
本稿では、それを少し拡張した広義積分
について考察する。 この値に関する一般的な公式は [6] にも紹介されているが、 ここでは、ディリクレ積分値と部分積分、三角関数の公式などを 用いて (2) を計算する過程を紹介する。竹野茂治@新潟工科大学