1 はじめに
以前、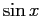 の導関数が
の導関数が 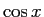 となることを、
極限ではなく図を用いて示す方法を紹介した ([1])。
一方、
となることを、
極限ではなく図を用いて示す方法を紹介した ([1])。
一方、
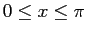 の範囲で、
の範囲で、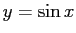 のグラフと
のグラフと 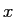 軸が囲む
部分の面積
軸が囲む
部分の面積 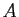 は、
は、
のように簡単な値である 2 になることが定積分によりわかるが、
これも易しく説明することはできないか、と考えてみた。
この面積は曲線で囲まれるため、円の面積の場合と同様、
ある程度は区分求積法の考え方、
すなわち細かく分けたものの和の極限のような見方は必要になるが、
とりあえずある程度易しい説明を見つけることができたので、
ここにまとめておく。
竹野茂治@新潟工科大学
2017年12月13日