1 はじめに

C 言語の、0 から RAMD_MAX¹ までの整数の乱数を返す rand() という関数を使って、例えばサイコロなどのように 1 から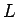

まで ( $L\ll \mbox{\tt RAND\_MAX}$ ) の整数をランダムに作り出したい場合、

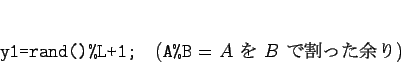$\begin{displaymath} \mbox{\tt y1=rand()\%L+1;}\hspace{1zw} (\mbox{{\tt A\%B} = $A$ を $B$ で割った余り})\end{displaymath}$ (1)

とするのが手っ取り早そうであるが、実はこれには問題がある。

以前 (少なくとも一部の rand() の実装では)、偶数と奇数が交互に生成される仕様になっていて、例えばサイコロの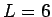の場合でも、 1,3,5 のいずれかと 2,4,6 のいずれかが交互に現われてしまうことになる。これではランダムとは言えないだろう。

これはもちろん rand() の実装自体に問題があるのであるが、この場合 (1) の代わりに、

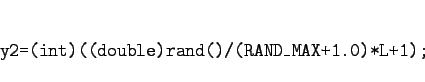$\begin{displaymath} \mbox{\tt y2=(int)((double)rand()/(RAND\_MAX+1.0)*L+1);}\end{displaymath}$ (2)

のような方法がよく用いられる。これは、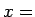

rand() に対し、

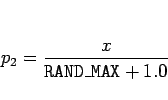$\begin{displaymath} p_2=\frac{x}{\mbox{\tt RAND\_MAX}+1.0}\end{displaymath}$ (3)

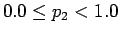によって $0.0\leq p_2<1.0$ の範囲の実数の乱数

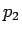を生成し、

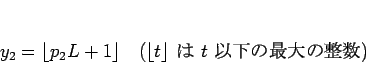$\begin{displaymath} y_2=\lfloor p_2L+1\rfloor\hspace{1zw} (\mbox{$\lfloor t\rfloor$ は $t$ 以下の最大の整数})\end{displaymath}$ (4)

によって 1 から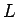

までの乱数を得る方法である。今回は、この方法の妥当性について検討してみることにする。

竹野茂治＠新潟工科大学
2007年6月22日