2 実際の確率と r とのずれ
以後、簡単のために RAND_MAX を 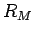 と書くこととし、
rand() の値を意味する
と書くこととし、
rand() の値を意味する 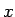 は、0 から
は、0 から 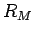 までの整数値を一様にとる
確率変数であるとする。
までの整数値を一様にとる
確率変数であるとする。
この場合、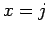 (
(
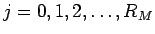 ) である確率はすべて等しいことになる
ので、
) である確率はすべて等しいことになる
ので、
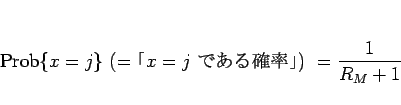 |
(1) |
となる。
1 節で紹介した方法では、
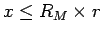 となるとき 1 となるようにしているが、
この確率
となるとき 1 となるようにしているが、
この確率
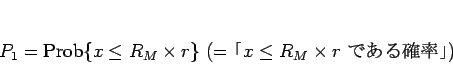
がほぼ 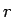 に等しいことが期待される。
に等しいことが期待される。
以下、まず一般の負でない実数 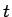 に対して、確率
に対して、確率
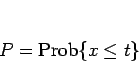
を 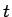 の式であらわすことを考えてみる。
の式であらわすことを考えてみる。
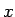 は実際には整数の値しか取らないので、
は実際には整数の値しか取らないので、
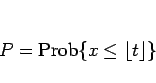
に等しい。ここで、
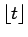 は、
は、
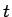 以下の最大の整数を表わすものとし2、
例えば
以下の最大の整数を表わすものとし2、
例えば
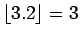 ,
,
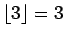 となる。
となる。
よって、(1) より、
となる。この公式 (2) を用いれば 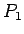 は
は
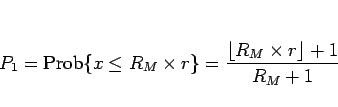 |
(3) |
となる。
ところで、
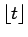 は定義、
あるいは図 1 のグラフより不等式
は定義、
あるいは図 1 のグラフより不等式
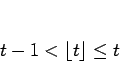 |
(4) |
を満たすことがわかる。
図:
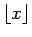 のグラフ
のグラフ
|
|
(3), (4) より、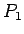 は
は
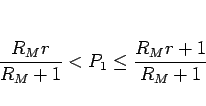
を満たすので、よって、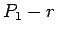 については
については
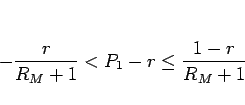 |
(5) |
が成り立つ。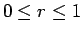 だから、
だから、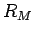 が十分大きければ
(5) の両端の値は十分 0 に近くなり、
よってそれなりに
が十分大きければ
(5) の両端の値は十分 0 に近くなり、
よってそれなりに 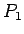 は
は 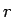 に近いことになる。
竹野茂治@新潟工科大学
に近いことになる。
竹野茂治@新潟工科大学
2007年5月31日
![]() (
(
![]() ) である確率はすべて等しいことになる
ので、
) である確率はすべて等しいことになる
ので、
![]() となるとき 1 となるようにしているが、
この確率
となるとき 1 となるようにしているが、
この確率
![]() に対して、確率
に対して、確率
![]() は定義、
あるいは図 1 のグラフより不等式
は定義、
あるいは図 1 のグラフより不等式