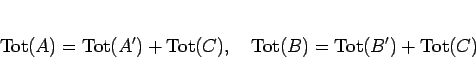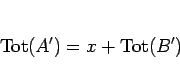3 主要命題の易しい証明
本節で、[1] の中心的な命題である命題 11 の易しい証明を紹介する。
命題 11 は以下の通り。
- 命題 11. ([1])
-
代金に対する最適解、
すなわち最終的に財布に残る小銭の枚数を最小にするような支払い方は
一意的に決まり、それ以外の支払い方では財布の小銭は最適解よりも
必ず多くなる。
この命題 11 は、そのような支払い方 (最適解) が
一意的であることの保証であり、最適解が存在することを
直接は保証はしていないが、
[1] では命題 3 から命題 10 にかけて最適解の構成の考察を行っていて、
実際には最適解の存在も (しかもその解の構成法も) 示している。
本稿では、この命題 11 を、命題 1 を用いて「逆」から考える。
まず、「非冗長解」を、「財布に残る小銭に冗長性がないような支払い方」
と定義する。これは、最適解の定義とは異なるが、
のちにこれが最適解と一致するものであることが示される (命題 13)。
なお、命題番号は、[1] とぶつからないように、
続きの番号から始める。
- 命題 12.
-
非冗長解が存在すれば、それは最適解となる。
- 証明
-
支払う額、そして支払う前の財布の中身が決まっていれば、
支払った後に財布に残る金額は、
支払い方によらずに一つの額に決定するはずである。
そして非冗長解の場合はその金額を冗長性がない形で
表現する小銭の集まりを作るが、
それが命題 2 により最小枚数の表現になるので、
よって非冗長解は最適解となる。
この命題 12 は、
非冗長解の存在を保証するものではなく、存在すればそれが最適解となる、
という主張であるから、非冗長解が最適解に完全に一致することは
まだ保証されていない。それは次の命題 13 で示される。
- 命題 13.
-
各代金に対して、非冗長解は常に存在する (よって非冗長解と最適解は常に一致する)。
- 証明
-
もとの財布の小銭の集まりを 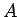 、支払い後の財布の金額の最小表現
(冗長でない表現) による小銭の集まりを
、支払い後の財布の金額の最小表現
(冗長でない表現) による小銭の集まりを 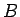 とする。
まず、札が必要ない場合を考える。
とする。
まず、札が必要ない場合を考える。
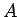 と
と 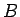 に共通に現れる小銭の集まりを
に共通に現れる小銭の集まりを 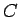 と書き、
と書き、
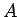 ,
, 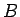 から
から 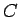 を除いたものをそれぞれ
を除いたものをそれぞれ 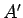 ,
, 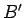 とする。
このとき、
とする。
このとき、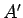 を支払えばおつりが
を支払えばおつりが 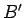 であることを示そう。
もし、それが言えれば、支払い後の財布の中身は
であることを示そう。
もし、それが言えれば、支払い後の財布の中身は 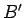 と
と 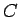 を
合わせた
を
合わせた 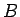 になり、よってこの支払いは非冗長解となる。
になり、よってこの支払いは非冗長解となる。
まず、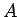 の合計金額
の合計金額
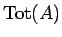 は、代金
は、代金 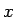 と
と
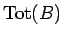 の合計
に等しいが、
の合計
に等しいが、
より、
となるので、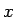 の代金に
の代金に 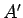 を支払えば、確かに
を支払えば、確かに
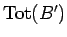 の
金額のおつりが返ってくる。
の
金額のおつりが返ってくる。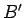 は
は 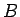 の一部だから、
当然冗長性はなく、よって仮定 4 と命題 1 の一意性により、
おつりは
の一部だから、
当然冗長性はなく、よって仮定 4 と命題 1 の一意性により、
おつりは 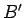 として返ってくるはずである。
として返ってくるはずである。
札が必要な場合も、上の式の左辺に札の金額 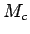 を追加するだけであり、
議論はほぼ同じである。
を追加するだけであり、
議論はほぼ同じである。
この命題 13 により、非冗長解が常に存在することが
構成的に示されたことになり、
そして命題 12 によりそれは最適解となる。
なお、命題 13 は、
非冗長解が一つしかないことは保証していないが、
その証明の考え方を用いれば、実はそれが一つであることも示される。
- 命題 14.
-
各代金に対して、非冗長解は一意に決定する。
- 証明
-
命題 13 の証明の記号をそのまま用いることとする。
札が必要ない場合を考えるが、札が必要な場合もほぼ同様であるので、
そちらは省略する。
命題 13 の証明の支払い方 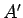 とは違う
支払い方
とは違う
支払い方 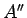 の非冗長解があるとすれば、
の非冗長解があるとすれば、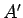 ,
, 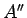 の 2 つの支払い方で
共に財布に残る小銭
の 2 つの支払い方で
共に財布に残る小銭 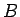 が同じになる。
この場合、
が同じになる。
この場合、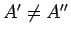 より、
より、
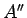 に
に 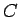 の一部が含まれるか、または
の一部が含まれるか、または 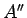 には
には 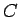 の小銭は
含まれないかのいずれかである。
の小銭は
含まれないかのいずれかである。
後者の場合、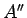 は
は 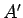 に完全に含まれることになり、
に完全に含まれることになり、
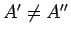 より、
より、
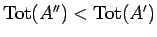 となる。
当然、そのおつり
となる。
当然、そのおつり 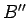 も
も
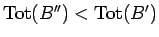 となるが、
一方、
となるが、
一方、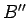 と支払わなかった小銭 (
と支払わなかった小銭 (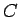 と、
と、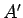 から
から 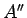 を除いたもの) が
最終的に残る小銭となる。
そしてそれが
を除いたもの) が
最終的に残る小銭となる。
そしてそれが 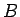 に一致するはずなので、
支払わなかった小銭のうち、
に一致するはずなので、
支払わなかった小銭のうち、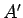 から
から 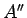 を除いたものは
を除いたものは 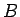 から
から 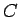 を
除いた
を
除いた 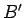 にも含まれていなければならない。
ということは、
にも含まれていなければならない。
ということは、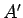 から
から 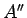 を除いたものは
を除いたものは 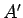 にも
にも 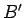 にも
共通に含まれていることになり、
それは
にも
共通に含まれていることになり、
それは 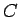 ,
, 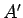 ,
, 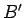 の定義に反する。
の定義に反する。
また前者の場合は、仮定 5 によって 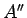 に含まれる
に含まれる 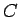 の一部は
おつり
の一部は
おつり 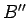 には含まれないことになるが、
その
には含まれないことになるが、
その 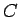 の一部は支払っている際の財布の中にもなく、
またおつりにも含まれないので、
の一部は支払っている際の財布の中にもなく、
またおつりにも含まれないので、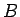 の中にも当然含まれないことになる。
しかし、これは
の中にも当然含まれないことになる。
しかし、これは 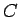 の定義に反する。
の定義に反する。
よって、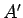 と違う払い方で結果が
と違う払い方で結果が 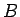 となることはないことが示され、
これにより非冗長解の一意性が示されたことになる。
となることはないことが示され、
これにより非冗長解の一意性が示されたことになる。
この命題 12, 13, 14 が、[1] の命題 11 の別証明にあたるが、
[1] の論法に比べてかなりシンプルになっている。
特に、[1] では多用した新しい記号による数式が、
こちらの証明の考え方ではほとんど必要がないことがわかる。
なお、一意性を示す命題 14 は最後にしたが、
これは [1] では示していない次の命題を用いれば、
一意性はすぐに従う。
- 命題 15.
-
支払い方が違えば、財布に残る小銭の集まりは必ず異なる。
- 証明
-
2 通りの支払い方を、下の位の硬貨から見ていって、
初めてその出し方が違う位の部分を考えると、
そこは一方は何枚か出し、他方はその位の硬貨は出してない、
という形になっているはずである。
それは、もし両者ともその位の硬貨を出していて、
その枚数が違っているとすると、それより下の位の硬貨は
同じものを出すわけだから、その位の硬貨の枚数の多い方は、
仮定 5 に反するからである。
その位の硬貨を何枚か出す方は、やはり仮定 5 によりおつりには
その額の硬貨は含まれないので、財布のその額の硬貨は必ず減ることになる。
一方、その位の硬貨を出さない方には、
そのおつりにその額の硬貨が必ず含まれる (それより下の位は
他方と同じものを出すので) から、
財布の中のその額の硬貨は必ず増えることになる。
よって、支払い方が異なれば、
財布に残る小銭の集まりは必ず異なることになる。
これは、支払い方が違えば、小銭の「集まり」が違う、ということで、
枚数が違うとまでは言っていないことに注意。
例えば、代金 11 円に、15 円支払うのと 51 円支払うのは、
どちらも 2 枚減って、おつりが 4 枚なので、違う支払い方だけれども
枚数は同じとなる (もちろんいずれも最適解ではない)。
竹野茂治@新潟工科大学
2017年12月20日
![]() 、支払い後の財布の金額の最小表現
(冗長でない表現) による小銭の集まりを
、支払い後の財布の金額の最小表現
(冗長でない表現) による小銭の集まりを ![]() とする。
まず、札が必要ない場合を考える。
とする。
まず、札が必要ない場合を考える。
![]() と
と ![]() に共通に現れる小銭の集まりを
に共通に現れる小銭の集まりを ![]() と書き、
と書き、
![]() ,
, ![]() から
から ![]() を除いたものをそれぞれ
を除いたものをそれぞれ ![]() ,
, ![]() とする。
このとき、
とする。
このとき、![]() を支払えばおつりが
を支払えばおつりが ![]() であることを示そう。
もし、それが言えれば、支払い後の財布の中身は
であることを示そう。
もし、それが言えれば、支払い後の財布の中身は ![]() と
と ![]() を
合わせた
を
合わせた ![]() になり、よってこの支払いは非冗長解となる。
になり、よってこの支払いは非冗長解となる。
![]() の合計金額
の合計金額
![]() は、代金
は、代金 ![]() と
と
![]() の合計
に等しいが、
の合計
に等しいが、
![]() を追加するだけであり、
議論はほぼ同じである。
を追加するだけであり、
議論はほぼ同じである。