2 設定

最初に、問題を考察する上での目標や設定、仮定などを上げておく。

本稿では、財布の中の小銭を減らすことを考え、 そこに関係するいくつかの基本的な問題を 数学的に考察することを目標とする。

仮定 1.

小銭を減らす、というのは、 代金の支払いにおいて、おつりの枚数を減らすだけではなく、 その代金に使用する小銭の枚数も同時に考えることとし、 すなわち個々の代金に対して、

(支払いに使う小銭の枚数) 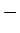$-$ (お釣りでもらう小銭の枚数)

を最大化することを考える。

仮定 2.

お札の枚数は考えない。 よって、代金は 1000円未満の小銭部分だけを考えればよい。 ただし、財布持ち金は代金を払うには十分あるとし、 よって、その小銭を払うために 1000円札も 1 枚は使えるとする。

仮定 3.

財布には無駄な小銭はないとする。 すなわち、1 円、10 円、100 円硬貨は最大で 4 枚まで、 5 円、50 円、500 円硬貨は最大で 1 枚しかないとする。

これは、代わりに次のような設定もありうるだろう。

仮定 $\mathbf{3}'$.

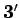財布の小銭は、表現が一意な形で入っているとする。 すなわち、5 円玉がなければ 1 円玉は 9 枚まで持てるとし、 さらに 10 円玉もなければ 1 円玉は 49 枚まで持てる等々。

さらに、次のような設定もありうる。

仮定 $\mathbf{3}''$.

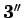財布の小銭には上限等の条件は特に設けない。

普段から気をつけて小銭を使っていれば、 財布の小銭を仮定 3 の状態に維持することはそれほど難しくはない。 よって、しばらくは仮定 3 のもとで考えることにする。

仮定 4.

おつりを返す店側には、 すべての種類の硬貨が常に必要な枚数揃っているとし、 店員もおつりの枚数が最も少なくなるように返してくれるものとする。

個々の代金について、財布の中からの支払い方 (支払う貨幣の組) を 解 と呼び、仮定 1 を満たす解を 最適解 と呼ぶことにするが、 そのような最適解が一通りであるかどうかは明らかではない。 もし一通りではない場合、最適解のうち、 例えば少額の硬貨がなるべく少なくなるような解を望ましい とする立場もあるかもしれないが、 とりあえずそこまでは考えないし、 むしろ最適解が一意的かどうかを先に検討したい。

仮定 5.

支払う硬貨の一部が、そのままおつりの一部として戻ってくる 払い方は解とはしない。

これは、もちろんその重なる部分を最初から除いて払えば それがおつりからも除外されるし、 そのように払っても最終的な硬貨の枚数も同じであるので、 そのような無駄 (非本質的な多重性) を排除するための仮定である。

なお、私もたまに間違えて仮定 5 を満たさないような 支払い方をすることがあり、その場合 通常店員に変な顔をされたり指摘されたりするが、 最近のコンビニなどでは何事もなくもレジを打って 普通に返してくれることもある。