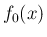
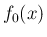 とする。
これは、
とする。
これは、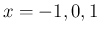 以外で定義される関数だが、ロピタルの定理により
以外で定義される関数だが、ロピタルの定理により
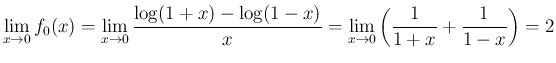
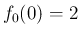 と定義すれば、
と定義すれば、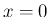 でも連続になる。
また、
でも連続になる。
また、
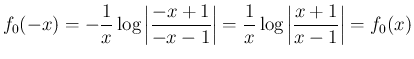
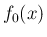 は偶関数なので、
主な性質に関しては
は偶関数なので、
主な性質に関しては 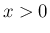 のみを考えればよい。
のみを考えればよい。
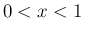 では
では
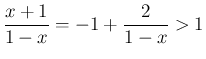
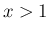 では
では
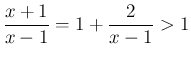
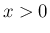 では
では 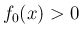 となる。
となる。
また、
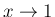 では、
では、
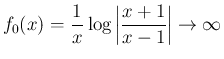
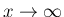 では、
では、
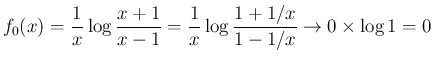
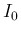 は、
は、
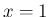 と
と 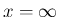 の 2 箇所に関して広義積分になっていることがわかる。
の 2 箇所に関して広義積分になっていることがわかる。
ただしそのオーダーを考えると、
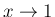 に関しては、
に関しては、
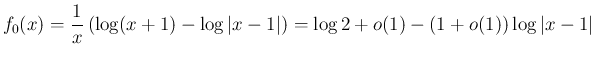
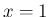 の付近では可積分、
の付近では可積分、
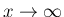 に関しては、
に関しては、
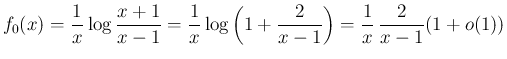
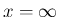 付近でも可積分となり、
よって (1) は有限な値に収束することがわかる。
付近でも可積分となり、
よって (1) は有限な値に収束することがわかる。
竹野茂治@新潟工科大学