4 パラメータの決定
式変形を行うために、以後、
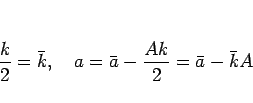 |
(6) |
と書いて、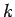 ,
, 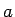 の代わりに
の代わりに 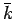 ,
, 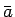 を決定することを考えることにする。
を決定することを考えることにする。
このとき、
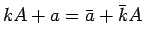 となるので、
となるので、
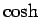 ,
, 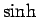 の加法定理 ([1] 参照) により、
(3), (5) の左辺は以下のようになる。
の加法定理 ([1] 参照) により、
(3), (5) の左辺は以下のようになる。
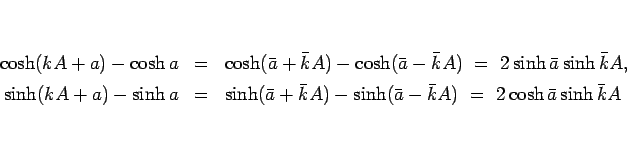
よって、(3), (5) は
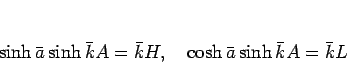 |
(7) |
と書ける。この (7) の両者の比を取れば、
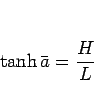 |
(8) |
となるので、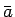 は
は
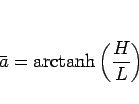 |
(9) |
と表されることになる。
ここで、
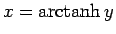 は、
は、 の逆関数 (詳しくは [1] 参照)。
の逆関数 (詳しくは [1] 参照)。
また、
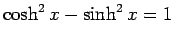 なので、
(7) の自乗の差を考えれば
なので、
(7) の自乗の差を考えれば
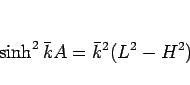
となり、よって 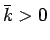 ,
, 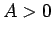 より
より
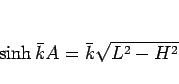
となる。この両辺を 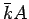 で割れば
で割れば
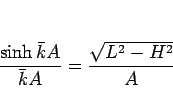 |
(10) |
が得られる。
ここで、
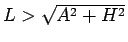 なので
なので 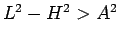 だから
この式の右辺は 1 より大きいことに注意する。
だから
この式の右辺は 1 より大きいことに注意する。
今、関数 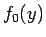 を
を
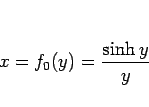
とすると、(10) は
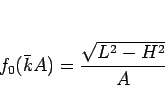
となるので、この 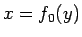 の逆関数
の逆関数 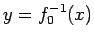 により
により 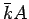 は
は
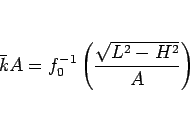
と書けるので、よって結局 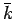 は
は
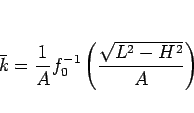 |
(11) |
と表されることになる。
なお、
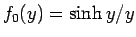 が、
が、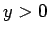 で単調増加であることは、
例えば
で単調増加であることは、
例えば 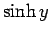 のマクローリン展開により示される。
のマクローリン展開により示される。
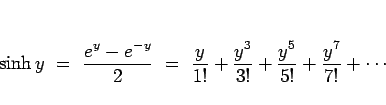
より
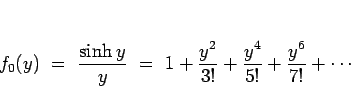
であるから、
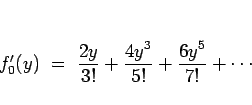
となり、この右辺は 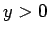 で正なので、よって
で正なので、よって 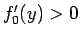 となる。
ゆえに
となる。
ゆえに 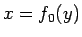 には逆関数
には逆関数 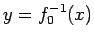 が存在することがわかる。
また、ロピタルの定理により
が存在することがわかる。
また、ロピタルの定理により
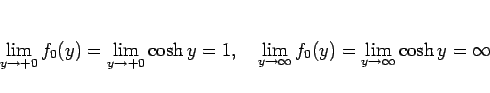
なので、
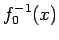 は
は 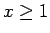 を定義域とし、
を定義域とし、
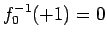 で、
で、
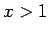 で滑らかになる。
よって、
で滑らかになる。
よって、
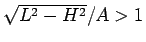 より (11) の右辺は一意に定まる正の実数値となる。
なお、
より (11) の右辺は一意に定まる正の実数値となる。
なお、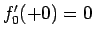 なので、
なので、
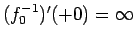 となっている。
となっている。
竹野茂治@新潟工科大学
2013年11月5日
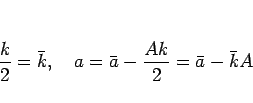
![]() となるので、
となるので、
![]() ,
, ![]() の加法定理 ([1] 参照) により、
(3), (5) の左辺は以下のようになる。
の加法定理 ([1] 参照) により、
(3), (5) の左辺は以下のようになる。
![]() なので、
(7) の自乗の差を考えれば
なので、
(7) の自乗の差を考えれば
![]() を
を
![]() が、
が、![]() で単調増加であることは、
例えば
で単調増加であることは、
例えば ![]() のマクローリン展開により示される。
のマクローリン展開により示される。