2 ある物体から受ける万有引力
まず、形と質量のある物体 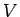 から、
点
から、
点 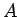 に置いた質量
に置いた質量 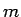 の小さい物体が受ける万有引力について考えてみる。
の小さい物体が受ける万有引力について考えてみる。
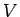 が、点 P に置かれた質量
が、点 P に置かれた質量 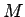 の小さい物体である場合、
点 A はその物体から、距離の 2 乗に反比例し、それぞれの質量に比例して、
互いに引き合う力である 万有引力
の小さい物体である場合、
点 A はその物体から、距離の 2 乗に反比例し、それぞれの質量に比例して、
互いに引き合う力である 万有引力
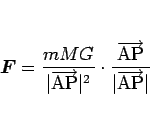
を受ける (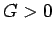 : 万有引力定数)。
なお、
: 万有引力定数)。
なお、
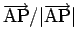 は A から P に向かう
単位ベクトルであることに注意する。
は A から P に向かう
単位ベクトルであることに注意する。
複数の点
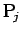 に質量
に質量 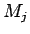 の小さい物体がある場合は、その合力
の小さい物体がある場合は、その合力
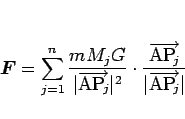
を受けることになる。
3 次元領域 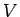 の場合は、
の場合は、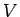 内の各点 P での密度を
内の各点 P での密度を
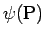 とすると、
とすると、
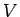 を小片
を小片 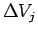 に分解して考えれば、
その小片の質量はほぼ
に分解して考えれば、
その小片の質量はほぼ
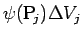 なので (
なので (
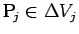 )、
)、
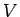 から
から 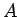 の物体が受ける万有引力は、
の物体が受ける万有引力は、
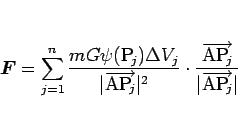
にほぼ等しく、厳密にはその極限としての体積分 (3 重積分) で表されることになる (積分変数は
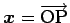 ):
):
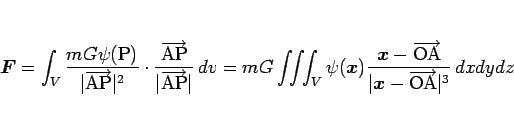 |
(1) |
この公式自体は、A が  の内部にあっても変わらないが、
その場合は分母が 0 となりうるので、
厳密には (1) は広義積分となる。
の内部にあっても変わらないが、
その場合は分母が 0 となりうるので、
厳密には (1) は広義積分となる。
さて、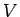 の重心点 Q の位置ベクトルは、
の重心点 Q の位置ベクトルは、
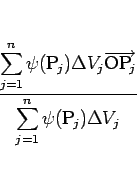
の極限として得られるので、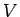 の総質量を
の総質量を 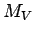 とすれば、
とすれば、
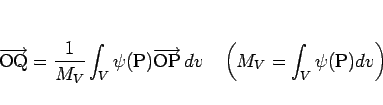
と表される。
よって、
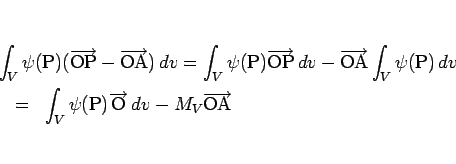
より、もし重心 Q に質量 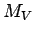 が集中していると考えると、
それが A におよぼす万有引力は、
が集中していると考えると、
それが A におよぼす万有引力は、
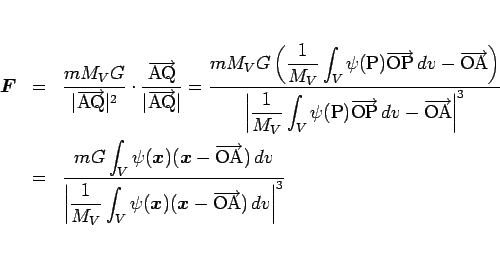
となるが、
これは (1) とは明らかに異なり、
一般に両者は等しくはない。
よって、重心に質量が集中していると考えてよいのは、
特別な場合であることがわかる。
竹野茂治@新潟工科大学
2013年1月6日
![]() が、点 P に置かれた質量
が、点 P に置かれた質量 ![]() の小さい物体である場合、
点 A はその物体から、距離の 2 乗に反比例し、それぞれの質量に比例して、
互いに引き合う力である 万有引力
の小さい物体である場合、
点 A はその物体から、距離の 2 乗に反比例し、それぞれの質量に比例して、
互いに引き合う力である 万有引力
![]() に質量
に質量 ![]() の小さい物体がある場合は、その合力
の小さい物体がある場合は、その合力
![]() の場合は、
の場合は、![]() 内の各点 P での密度を
内の各点 P での密度を
![]() とすると、
とすると、
![]() を小片
を小片 ![]() に分解して考えれば、
その小片の質量はほぼ
に分解して考えれば、
その小片の質量はほぼ
![]() なので (
なので (
![]() )、
)、
![]() から
から ![]() の物体が受ける万有引力は、
の物体が受ける万有引力は、
![]() の重心点 Q の位置ベクトルは、
の重心点 Q の位置ベクトルは、