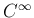
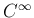 関数の積に対して、積の微分が成り立つかどうかを見ておく。
関数の積に対して、積の微分が成り立つかどうかを見ておく。
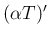 と
と
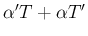 を比較すると、
を比較すると、
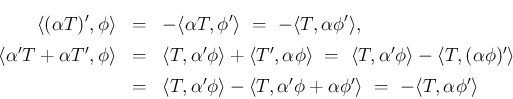
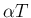 に対する積の微分は成立する。
に対する積の微分は成立する。
次に、(7) であるが、これも
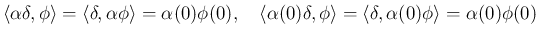
となれば、(8) と (9) で
矛盾が起きているように思うかもしれないが、そこに一つ見落しやすい誤解がある。
それは、(7) とは違い、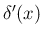 に対しては
に対しては
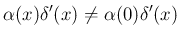
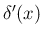 も
も 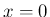 でしか値を持たないものなので、
なんとなく
でしか値を持たないものなので、
なんとなく
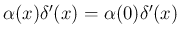 は
正しく感じるかもしれないが、実際には、
は
正しく感じるかもしれないが、実際には、
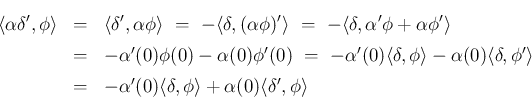
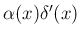 は
となるのである。
は
となるのである。
実際、これを (8) の 2 つ目の式に代入すれば、 (9) が得られるので何も矛盾は起こらない。
竹野茂治@新潟工科大学