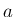 (
(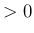 ) だけ距離をあけた曲線は、
元の曲線に「相似」な円となるが、一般の曲線の場合は必ずしもそうではない。
) だけ距離をあけた曲線は、
元の曲線に「相似」な円となるが、一般の曲線の場合は必ずしもそうではない。
円の場合は、外に 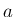 (
(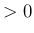 ) だけ距離をあけた曲線は、
元の曲線に「相似」な円となるが、一般の曲線の場合は必ずしもそうではない。
) だけ距離をあけた曲線は、
元の曲線に「相似」な円となるが、一般の曲線の場合は必ずしもそうではない。
例えば、正方形の場合でも、「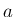 だけ距離を開けた曲線」は、
実は前節の相似な正方形ではなく、四隅を円弧に置き換えたものに
なる (図 5)。
だけ距離を開けた曲線」は、
実は前節の相似な正方形ではなく、四隅を円弧に置き換えたものに
なる (図 5)。
ちなみに、この場合は 2 つの曲線の周長の差は、四隅の円弧の部分に
なり、そこから半径 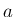 の円が構成できるので
の円が構成できるので 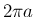 となり、
円の場合の差 (1) に一致にする。
そしてこの値は、実は正方形に限らず、一般の四角形でも、
また三角形でも成立する (図 6)。
となり、
円の場合の差 (1) に一致にする。
そしてこの値は、実は正方形に限らず、一般の四角形でも、
また三角形でも成立する (図 6)。
これがより一般の曲線の場合にも成立するのかを考えてみる。
竹野茂治@新潟工科大学