三角波による音声データ (WAV 176444Byte: 4 秒)

ノコギリ波による音声データ (WAV 176444Byte: 4 秒)

方形波による音声データ (WAV 176444Byte: 4 秒)
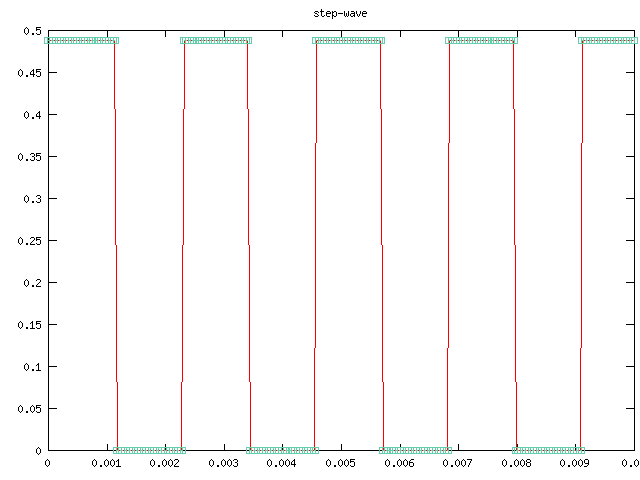
以下の各音声データは、基本的な周期関数である三角波、ノコギリ波、 方形波を用いて、特定の音声データを作成したものです。
そして、そのグラフは、それらの音声の先頭部分 (0.01 秒間) の部分 を表示したものです。赤い曲線で書かれているのが元となる周期関数で、 実際の音声データファイル (WAV format, サンプリング周波数 22050Hz, 16bit 量子化) には、四角で表されている点のデータのみが納められて います。
聞き比べてみてください。



講義中に紹介した、ノコギリ波、方形波に対するフーリエ級数のグラフを 紹介します。
ノコギリ波に対するフーリエ級数は
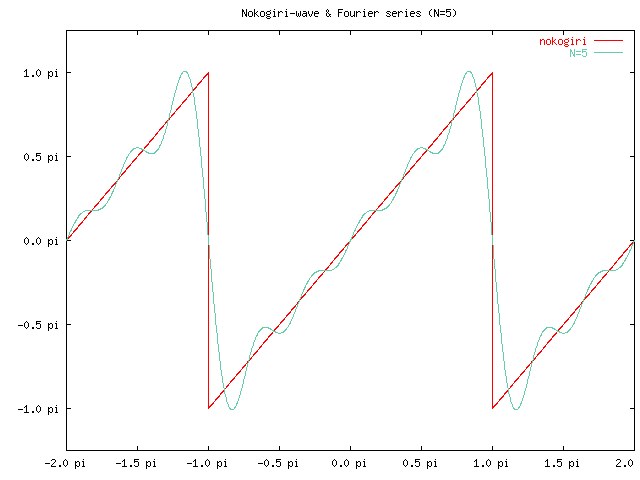
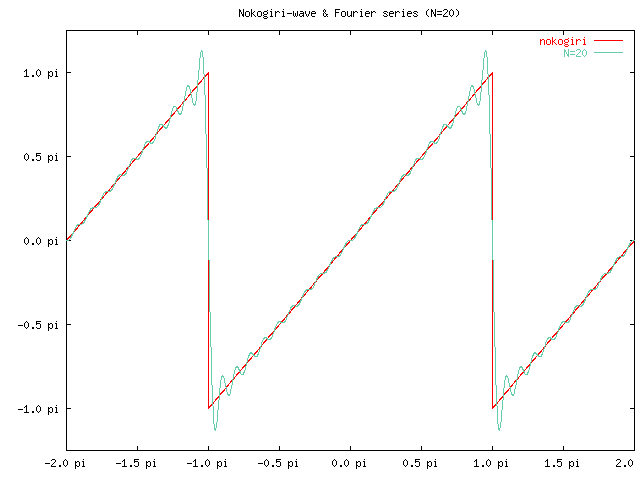
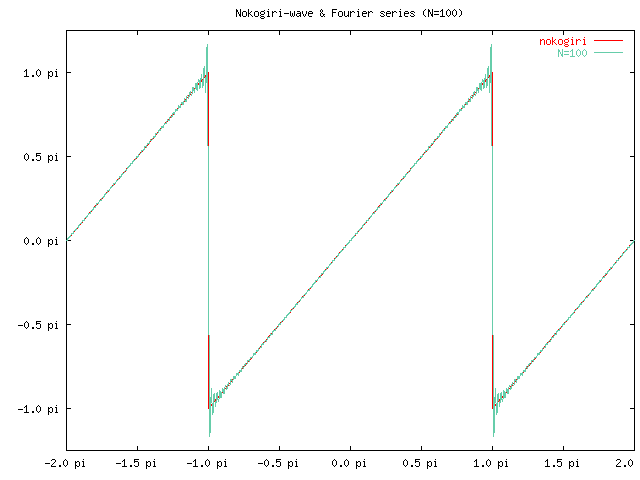
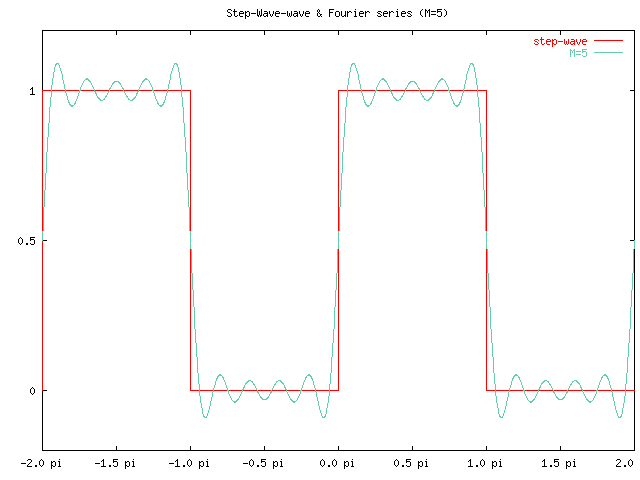
でした。このフーリエ級数の最初の N 個の和のグラフを、 ノコギリ波のグラフと重ねたものを以下に紹介します。
フーリエ級数が、徐々にノコギリ波に近づいていく様子が見えますが、 特徴的なのは、不連続点の近くではグラフの振動が大きくなり、 N を大きくなるとそれは徐々に不連続点の方に寄りますが、 一定の大きさの誤差であり続ける、ということです。 これがギブス現象と呼ばれる現象です。 この誤差は両側でそれぞれ段差の約 9% (=0.0894898...) になることが 知られています。

方形波に対するフーリエ級数は
でした。このフーリエ級数の最初の M 個の和のグラフを、 方形波のグラフと重ねたものを以下に紹介します。

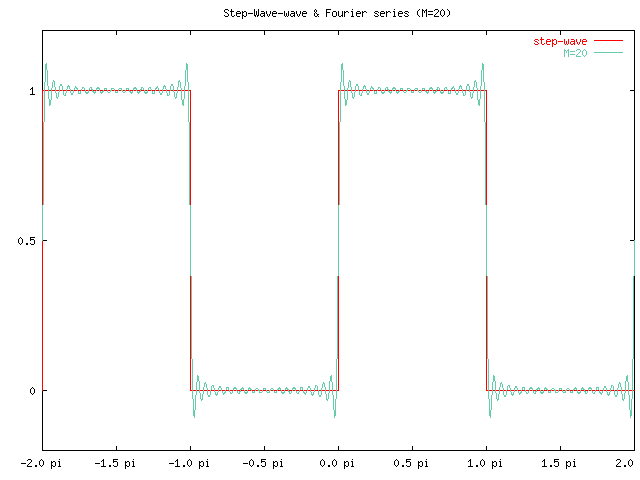

さて、三角波、ノコギリ波、方形波の音はかなり違った音であることは 前に紹介しましたが、 例えばノコギリ波に対して、それをフーリエ級数の部分和で徐々に近似 していくと、グラフは三角波から徐々にノコギリ波に近づいていきますが、 音としても三角波の音からノコギリ波の音に近づいていくでしょうか。 その途中の音はどんな音になると思いますか。
(12/17 2000)これは直接講義の内容とは関係ありませんが、ついでに作った音声データです。 元ネタは安野光雅さんの「算私語録」(朝日文庫) の 341 です。
例えば音がテープに録音されているとして、その先頭の位置を 0, 最後
の位置を 1 とします。1 から 0 に再生すれば、よくある逆回しになります。
それを、全体を 2 等分して、0.5 から 0, 1 から 0.5 と続けて再生すると、
前半分と後ろ半分は相変わらず逆回しのままですが、若干音の位置は
元の位置に近くなります。
さらに 4 等分して、0.25 から 0, 0.5 から 0.25, 0.75 から 0.5,
1 から 0.75 とするとそれぞれは相変わらず逆回しなのですが、
徐々に音が元の位置に戻って来て、段々元の音に近付いて行きます。
これを延々繰り返したらどうなるか、というのがそのお話です。
で、そこにはパリ在住のピョートル・コワルスキー (Piotr Kowalski)
という人がそれを行った、と書いてあります。
デジタルサンプリングされた音声データだと、何回かやると完全に 元のものと同じになってしまうので、本当はアナログデータでやらないと 面白味がないのですが、取りあえずそれをやってみたのが下のデータです。
元の音源は、音声データをフリーで公開している こえうぇぶ の音声データの 一部分、及びそれらをつなげたものを使用しています。
最初に聞こえるのが単なる逆回し、それを徐々に 2 分割、4 分割、 としていって、最後に聞こえるもの (65536 分割) が元のデータと 同じものです。
ただ難点は、元のデータが透明すぎて (特に母音だけの方)、最初のものが 全然逆回しに聞こえないことです (^^;
目次に戻る補講で紹介した、三角波以外の正規直交系のグラフを紹介します。
まずは
のグラフです。
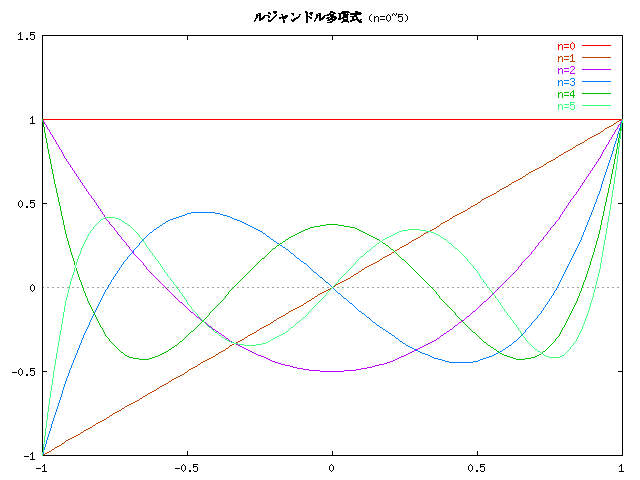
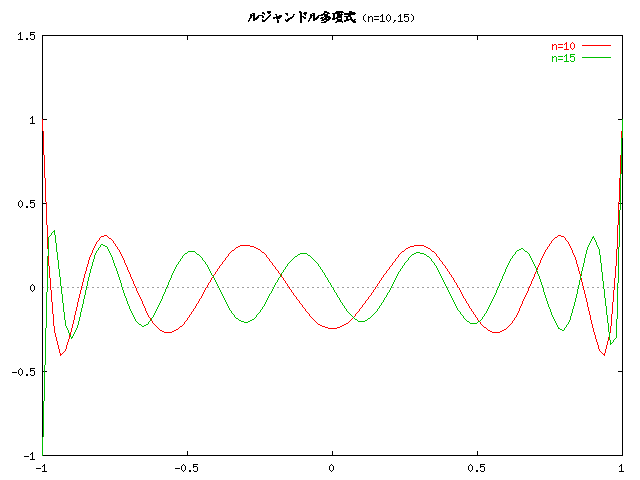
なお、ルジャンドル多項式は、次のような漸化式で計算することも できます。
コンピュータ等で計算する場合はこちらの方が実用的でしょう。 しかし、再帰的定義を使うと、大きい n に対してはあまり実用的では なくなりますので、再帰を使わないようにする必要があります。
ルジャンドル多項式は次のように正規化されます。
この関数のグラフを紹介します。
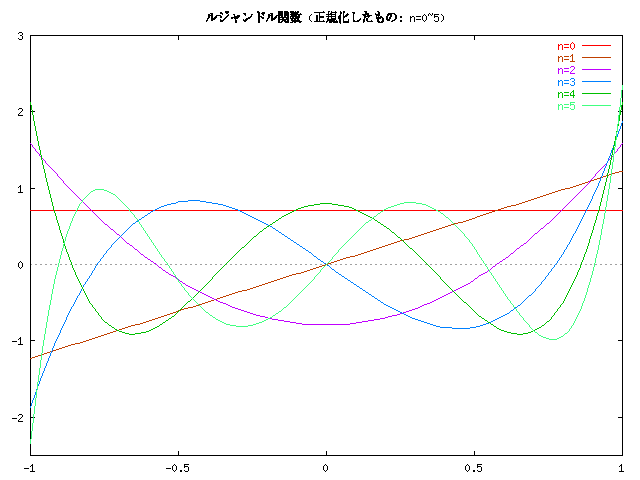
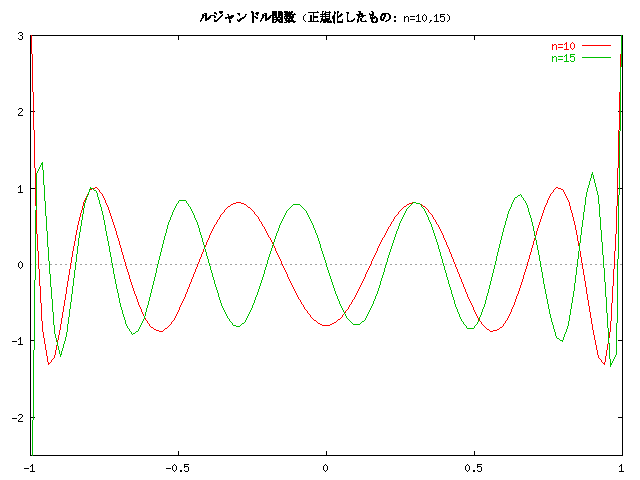
次は
です。漸化式は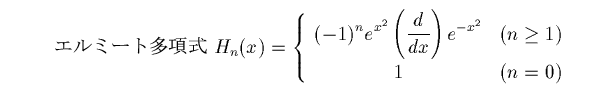
であり、次のようなものが正規直交系になります。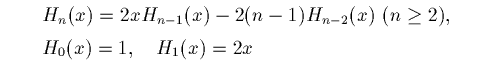
この正規直交系のグラフです。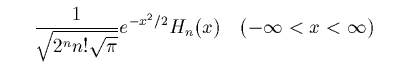


最後は
です。漸化式は
であり、次のようなものが正規直交系になります。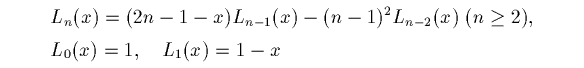
この正規直交系のグラフです。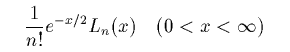
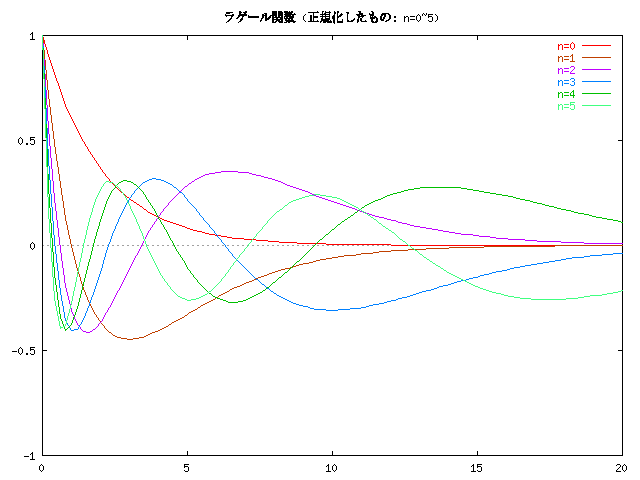

いずれの正規直交系も、n が増える度に一つずつしわが増えるような関数系に なっていることがわかります。そしてエルミートやラゲール関数の場合には、 そのしわが段々全体に広がって行きます。 逆にいうと、関数系の完全性のためには、そういうしわが必要だということ になるのでしょうか。 三角関数系の場合も n が増えると段々しわが増えていき、周波数が増して いきますが、丁度それに対応します。
なお、数学辞典によると、ラゲール多項式は 0<x<∞ での広義積分の値の 数値計算で使われ、エルミート多項式は統計学でも使われるそうです。 ルジャンドル関数は、波動方程式やラプラス方程式と呼ばれる重要な方程式の 固有関数を数式であらわすことなどに使われます。
(02/20 2001)ついでに、フーリエ級数の例としてワイヤストラスの関数を紹介します。
ワイヤストラス (K.T.W.Weierstrass 1815-1897 独) は「厳密の権化」、 「近代解析学の父」と呼ばれたほど、解析学の色々な分野の厳密的な 仕事に関わった数学者ですが、次のような関数の例を構成しています。
連続だが、すべての点で微分可能でない関数が存在する「連続」はグラフがつながっていることを意味し、「微分可能でない」は グラフに接線が引けないこと、つまりグラフがとがったりしていることを 意味しています。 例えば、絶対値関数 y=|x| は連続ですが、x=0 では微分可能ではありません。
また、例えば次のような関数 (ディリクレの関数と呼ばれることもあります)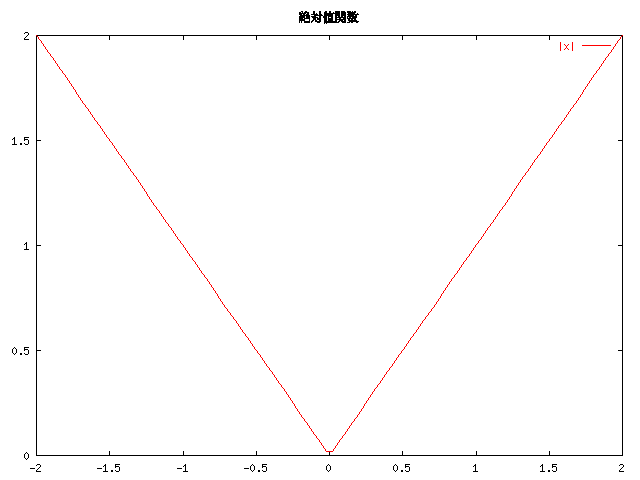
はすべての点でとがっているようですが、これは連続ではありません。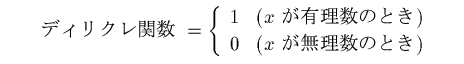
普通の「連続」な関数は、「微分可能」でない点は有限個しかありません。 しかし、ワイヤストラスは全ての点でグラフがとがっていて、かつ連続で あるような例を、フーリエ級数の形で与えました。
a=1/2, m=13 のとき、この級数の第 N 部分和 (n=1 から n=N までの和) のグラフは次のようになります。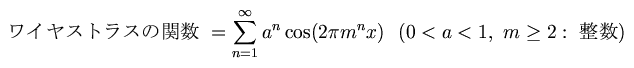
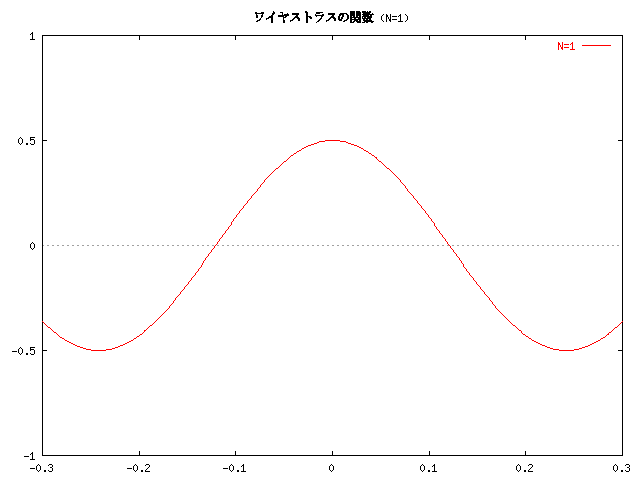
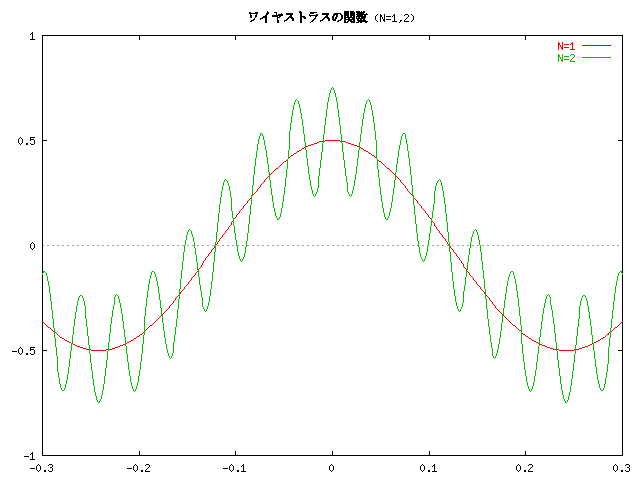
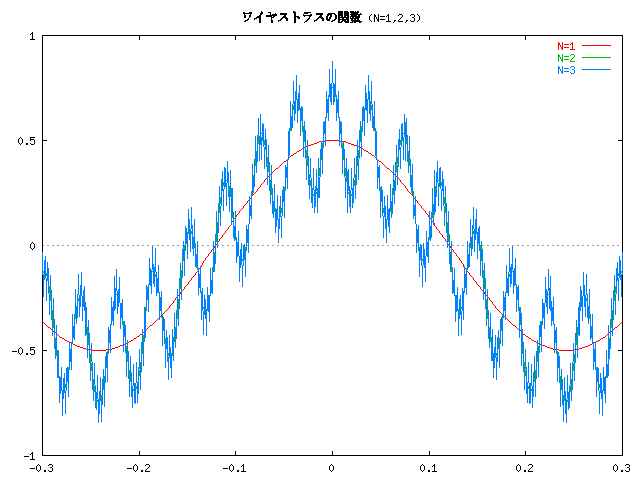
逆に考えると、フーリエ級数は、こんなとんでもない関数でも展開できて しまうほど、表現力、自由度が豊かだ、ということになります。 テイラー展開が無限回微分可能な関数でないと使えないのに比べると、 これは大きなメリットだといえるでしょう。 また、このグラフは、いわゆる "フラクタル" の例にもなっています。
なお、ワイヤストラスは 40 才までは中学校の先生をしていて、その後 大学の研究職についた人で、一流の数学者としては珍しく 大器晩成な人としても知られています。
(02/20 2001; 08/19 2008 修正)追加ですが、ついでに上のグラフの N=1, N=2, N=3 のグラフを tbl2snd を用いて音にしてみました (いずれもサンプリング周波数 11025Hz, 16bit linear WAV file)。
音の震えのようなものが徐々に増えていく感じが聞こえると思います。
(12/28 2009)妙なタイトルですが、少し変なことを考えつきましたので紹介します。
このページの上の方に、単純な音とそのグラフを紹介していますが、 具体的な音である、「あ」の音のグラフを紹介しましょう。
とげのようなもので構成されていて、グラフの様子がよくわかりませんが、 そのとげ一つ一つが基本周期部分です。 実際の音の場合は、 全く同じ形の基本周期がずっと繰り返されるわけではありませんが、 音質のあまり変わらない部分ではだいたい似た形の関数が繰り返されています。 上のグラフの一部を拡大して見てみます。
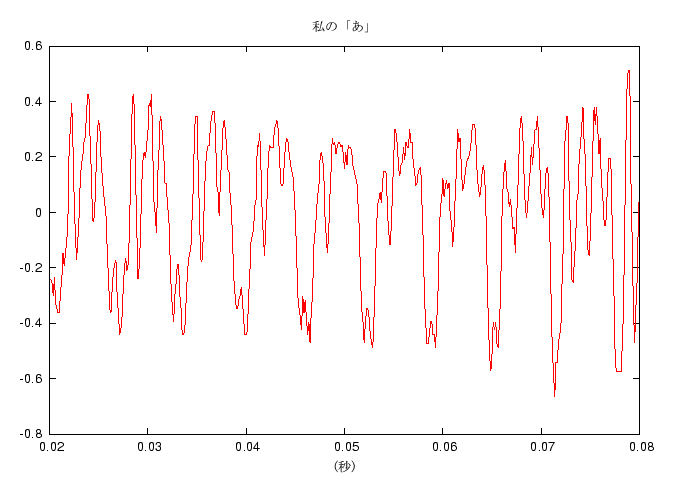
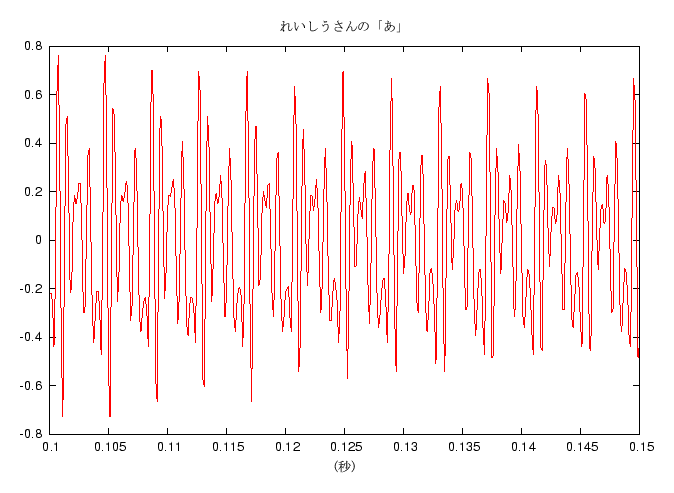
れいしうさんのグラフの方がきれいに同じ形のグラフが並んでいますが、 それは、れいしうさんの方が声が一定できれいな声であることと、 れいしうさんの声の方が高いことに原因があります。 同じ時間の「あ」でも、高い音の場合は周波数が高い、 すなわち基本波形の繰り返しが多く (れいしうさんのは 0.05 秒間で約 12 回、わたしのは 0.06秒間で約 9 回)、 声のように出だしから最後までの間に音が変化するものだと、 低い声の場合は少ない繰り返しでその変化を行わなければいけません。 よって、低い声の場合は同じ波形の繰り返しはあまり続きません。 (しかし、だからといって、低い声よりも高い声の方が聞きやすいことになる、 のかどうかは私にはわかりません)
もう少し拡大してその基本波形のグラフを見てみます。 基本波形 2 つ分くらいのグラフを紹介します。
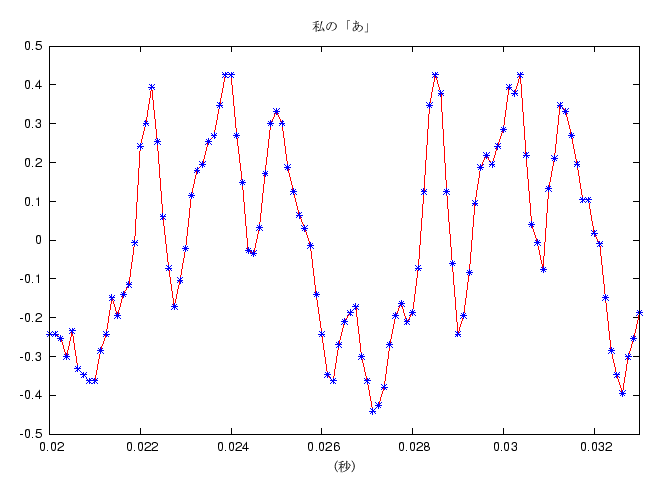
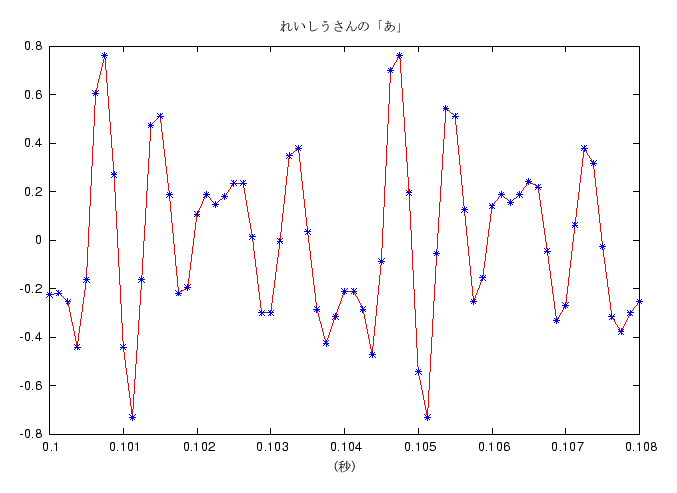
実際には音のデジタルデータには、 グラフの青い点のところだけのデータが保存されていて (このデータの場合は 1/8000 秒毎)、 このグラフはその青い点を折れ線で結んでいるだけです。
さて、上の音は「「あ」の音」ですし、 そのグラフは「「あ」の音」のグラフなわけですが、 私はグラフを音声化するソフトを持っています。 それはグラフの高低を音程の高低で表現するソフトです。
これを使うと、このグラフを音にすることができます。 つまり「「あ」の音」の音です。 実際に、上の基本波形 2 つ分のデータを音にしたものが以下のデータです。ということは、同じことをさらに繰り返せば、 「「「あ」の音」の音」の音、「「「「あ」の音」の音」の音」の音、 とかできるのですが、 実は、「「「あ」の音」の音」の音より先はあまりおもしろくありません。
「「あ」の音」の音を聞いてみればわかるのですが、 これは単純な音、つまり三角波 (正弦波) を元にして作られています。 上のグラフを音声化するツールは、 グラフの高いところでは三角関数の周期を短くして高い音を作り (高さや波形は変えずに横幅だけ短くする)、 グラフの低いところでは逆に周期を長くして低い音を作っています。
つまり、「「「あ」の音」の音」のグラフは
三角関数のグラフと見た目がほとんど変わらず、
一番低いところと高いところの同じところを振動しているだけで、
その振動が速くなったり遅くなったりしているだけです。
ということは、「「「あ」の音」の音」の音は、
「三角関数のグラフ」の音
(
gnuplot グラフの音声化ツール tbl2snd のサンプル参照)
とほとんど同じになってしまいます。
(04/04 2006)
先日、TV 番組の「探偵ナイトスクープ」で、 「名探偵コナン」に出てきた DTMF 信号を人間の声で本当に再現できるか、 ということをやっていました。 DTMF 信号というのは、 プッシュホンの電話で電話の番号一つ一つに割り当てられている音で、 プッシュホンは実際にその音を送信することで番号を送っているのだそうです。 実際には DTMF は、以下のような 2 種類の音の「和音」として 構成されているようです。
| 低音\高音 (Hz) | 1209 | 1336 | 1477 | 1633 |
|---|---|---|---|---|
| 697 | 1 | 2 | 3 | A |
| 770 | 4 | 5 | 6 | B |
| 852 | 7 | 8 | 9 | C |
| 941 | * | 0 | # | D |
A,B,C,D はよくわかりませんが、 このような 2 種類の音の和音は、 「yomi」 の付属ツールである sndhz と sndmix, wavconn で簡単に作成ができます。 例えば、以下の通りです。
sndhz -c1 -wav -v0 440 200 > null.wav (0.2 秒の無音)このようにして作成した音声データを以下に置きます (0.8 秒の音声 + 0.2 秒の無音、モノラル、WAV, 22094 byte)。
sndhz -c1 -wav 697 800 > tmp.wav (0.8 秒、697Hz)
wavconn ./tmp.wav ./null.wav > 697.wav (それを連結した 1.0 秒データ)
sndhz -c1 -wav 1209 800 > tmp.wav
wavconn ./tmp.wav ./null.wav > 1209.wav (同様の 1209Hz, 1.0 秒データ)
sndmix 697.wav 1209.wav > dtmf-1.wav (和音データ)
dtmf-0.wav (0), dtmf-1.wav (1), dtmf-2.wav (2), dtmf-3.wav (3), dtmf-4.wav (4),
dtmf-5.wav (5), dtmf-6.wav (6), dtmf-7.wav (7), dtmf-8.wav (8), dtmf-9.wav (9),
dtmf-A.wav (A), dtmf-B.wav (B), dtmf-C.wav (C), dtmf-D.wav (D),
dtmf-ast.wav (*), dtmf-sha.wav (#)
実際に、この音声を PC で再生したものを手元の電話の通話口に聞かせてみたら、
本当につながりました。
ただ、ノイズの関係か、タイミングの問題か、
高低の音のバランスの関係かはわかりませんが、
実際につながるのは 3 回に 1 回程度のようでした。
(06/12 2009)
「ドレミファソラシド」の音階には、 それぞれの音に対応した周波数が割り当てられているのですが、 実はその割り当て方 (=音律) にはいくつかの方式があります。
現在日常的によく使われているのは「平均律」と呼ばれるものですが、 その他にも「ピタゴラス音律」「純正律」「中全律」などもあるようです。 詳しくは、例えば以下を参照してください。
音律の仕組みを最初に発見したのは、 三平方の定理でも有名なピタゴラスであるとされていて、 ピタゴラスは弦を弾いて音を出す場合、 弦の長さを半分にすると音が 1 オクターブ (半音 12 個分) 上がり、 1/3 にすると 1 オクターブと完全 5 度 (半音 12+7 個分、ドと 1 オクターブ上のソの関係) 上がることを発見しました。 これは周波数で言えば、周波数を 2 倍にすると 1 オクターブ、 3 倍にすると 1 オクターブと完全 5 度上がることを意味します。 この、「3 倍することで 5 度上げる」「半分にすることで 1 オクターブを下げる] という作業の組み合わせですべての音階を作成したのが「ピタゴラス音律」です。
ピタゴラス音律の場合の「ド、レ、ミ、ファ、ソ、ラ、シ、ド」の周波数の比は 以下のようになります。
1, 9/8, 81/64, 4/3, 3/2, 27/16, 243/128, 2ただし、ファの音だけは、3n/2m の形をしていませんが、 それは分子、分母が大きくなりすぎないように、 上のドから逆に 5 度下げることでファを得ているために 4/3 となっています。
しかし、和音は簡単な整数比の音の方がまざりやすいのですが、 ピタゴラス音律はミ、ラ、シの周波数の分母が大きいため、 それを含む和音が綺麗にまざり合いにくい、という欠点があります。 それを改良したのが「純正律」で、それは以下のような比率になっています。
1, 9/8, 5/4, 4/3, 3/2, 5/3, 15/8, 2しかし、純正律は転調すると比が合わなくなりますので、 楽譜の調に合わせて調律を変えなければいけませんし、 曲中の転調には対応できません。 そこで作られたのが「平均律」で、 これは半音間隔をすべて等分にしたものです:
1, a2, a4, a5, a7, a9, a11, 2これはいずれも整数比ではないので、 和音には必ずうなりが含まれることになりますが、 例えば調を簡単に変更できないピアノなどは平均律に調律されています。 この他にも、前掲書によれば「中全律」なるものもあるようです:
(a=21/12)
1, b2/2, 5/4, 2/b, b, b3/2, b5/4, 2以上は長音階ですが、短音階 (自然短音階:「ラ、シ、ド、レ、ミ、ファ、ソ、ラ」) では以下のようになります。
(b=51/4)
これを小数で書くと以下のようになります。
| 長音階 | ||||
|---|---|---|---|---|
| ピタゴラス | 純正律 | 平均律 | 中全律 | |
| ド | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
| レ | 1.125000 | 1.125000 | 1.122462 | 1.118034 |
| ミ | 1.265625 | 1.250000 | 1.259921 | 1.250000 |
| ファ | 1.333333 | 1.333333 | 1.334840 | 1.337481 |
| ソ | 1.500000 | 1.500000 | 1.498307 | 1.495349 |
| ラ | 1.687500 | 1.666667 | 1.681793 | 1.671851 |
| シ | 1.898438 | 1.875000 | 1.887749 | 1.869186 |
| ド | 2.000000 | 2.000000 | 2.000000 | 2.000000 |
| 短音階 | ||||
| ピタゴラス | 純正律 | 平均律 | 中全律 | |
| ラ | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
| シ | 1.125000 | 1.125000 | 1.122462 | 1.118034 |
| ド | 1.185185 | 1.200000 | 1.189207 | 1.196279 |
| レ | 1.333333 | 1.333333 | 1.334840 | 1.337481 |
| ミ | 1.500000 | 1.500000 | 1.498307 | 1.495349 |
| ファ | 1.580247 | 1.600000 | 1.587401 | 1.600000 |
| ソ | 1.777778 | 1.800000 | 1.781797 | 1.788854 |
| ラ | 2.000000 | 2.000000 | 2.000000 | 2.000000 |
普通に音階を聞くだけではあまり違いがわからないと思いますが、 重ねたり、和音にするとうなりによってその違いなどがわかります。 そのような音のサンプルを yomi のツールで作ってみましたので、 以下に紹介します。 いずれも WAV ファイル (サンプリング周波数 11025Hz) です。 なお、基音をド位 (262Hz) にしてハ長調、イ短調の音階にすると、 下の方の音がやや低すぎて音が小さく聞こえるので、 基音をファ位 (349Hz) にしてヘ長調、ヘ短調にしてあります。
同じ音を重ねたものは、違いがうなりとして聞こえるのでよくわかると思います。 うなりがゆるやかなほど音が近く、 うなりが早いほど音が離れていることを意味しています。
また、ドミソとドファラの和音は純正律が一番響きがよく、
後は多分ピタゴラス、中全律、平均律の順に響きが悪くなっているはずですが、
違いはわかるでしょうか。
(02/01 2010)
楽器や声などの現実の音は、はっきりある音程に聞こえる音でも、 単音ではなくて複数の音の重ね合わせで作られていることが知られています。 特に、特定の音程が出せる楽器の場合は、 その重ね合わせは、その音程を基音として、 基本的にはその音のオクターブ上の音が順に重ね合わされています。
つまり、ある音にその音の丁度オクターブ上の音を重ねると、 それは「複数の音からなる和音」ではなく、 「音色のついた一つの音」として聞こえることになります。 重ね合わせる各音をどのような大きさにするかで、 その音の「音色」が決まるわけです。
なお、別な音程の音が重なれば「和音」になってしまうわけですが、 実際には楽器の音などは丁度オクターブ上の同じ音だけが重なっているわけではなく、 基音の 2 倍 (1 オクターブ上)、3 倍、4 倍 (2 オクターブ上)、5 倍、... といった周波数の音、いわゆる「倍音」が重なっています。 それは楽器の構造、音の出る仕組みからそのようになっています。
ところで、これに関して、ふと 「人間の耳はその音色に関して位相のずれを認識しているのか」 ということが気になりました。
例えば、ある周波数ωの単音 A sin(2πωt) (t は時刻、A は振幅) に対して、その 1 オクターブ上の音は
B sin(4πωt) + C cos(4πωt) = D sin(4πωt+θ) (D = (B2+C2)1/2)の形で表されますが、この音は cos の成分のために元の音 A sin(2πωt) と位相がθだけずれています。 この場合、もちろん
A sin(2πωt) + D sin(4πωt+θ)と
A sin(2πωt) + D sin(4πωt)とはグラフは別なものになりますが、 人間の耳はこれを別の音として認識するのだろうか、 というのが私の疑問です。
人間の耳は、蝸牛によって音を周波数分解して認識しています。 ということは人間は位相のずれは理解せず、 上の 2 つを同じ音として聞いているのではないか、 というのが私の予想でした。 それで以下のようなデータを作って試してみました。
c1.wav は 1 ブロックが 1/21.12 周期なので、 10 ブロックのずらしでほぼ元の c1.wav の逆位相の音になります。 0 から 9 ブロックのずらしでだいぶ異なったグラフができると予想されます。 実際にそれによって作成した音声データと、 その重ね合わせ音声のグラフを以下に示します。
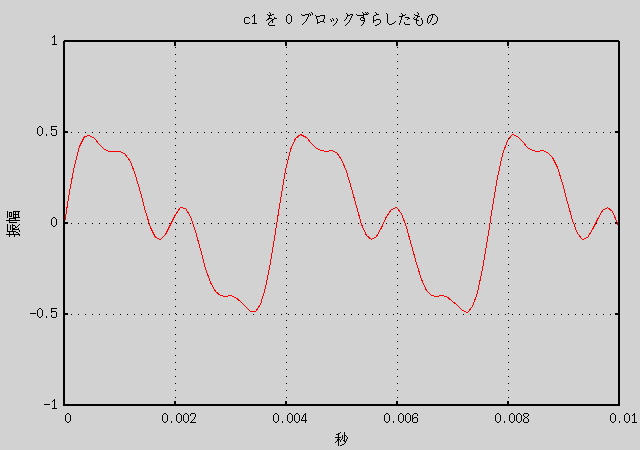
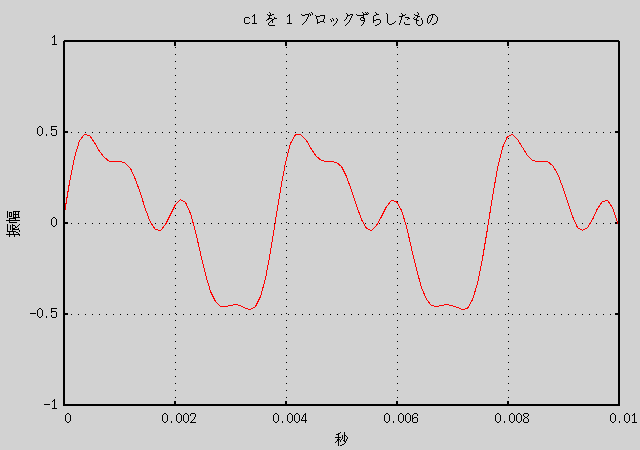
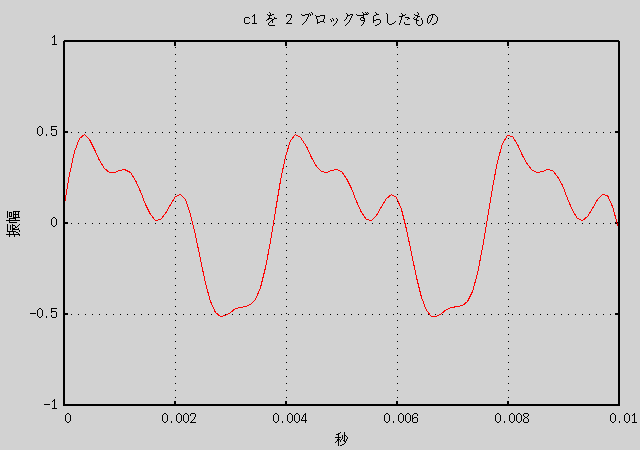
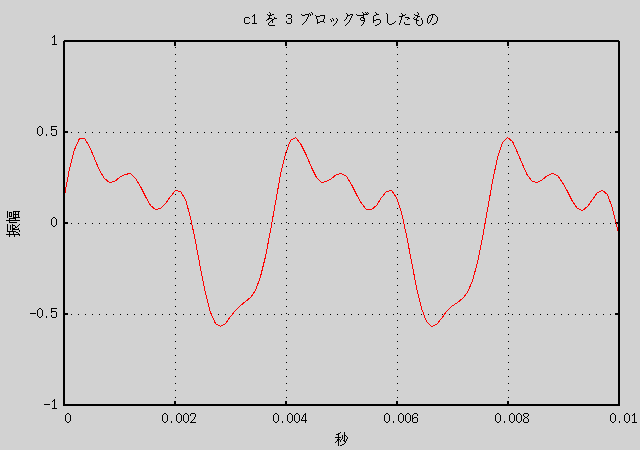
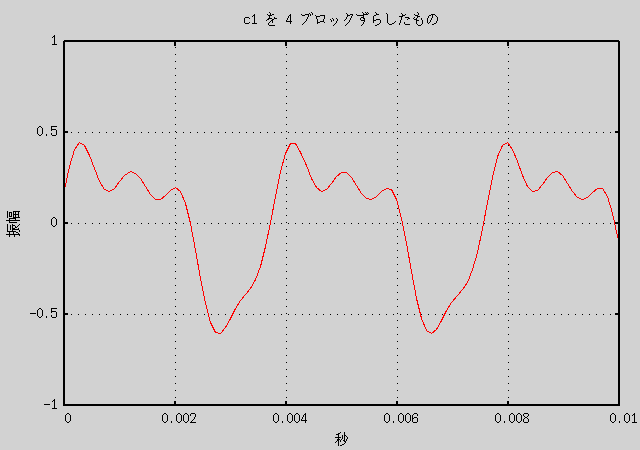
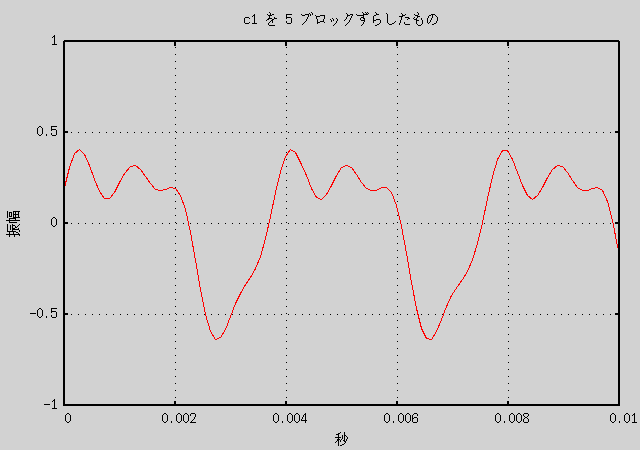

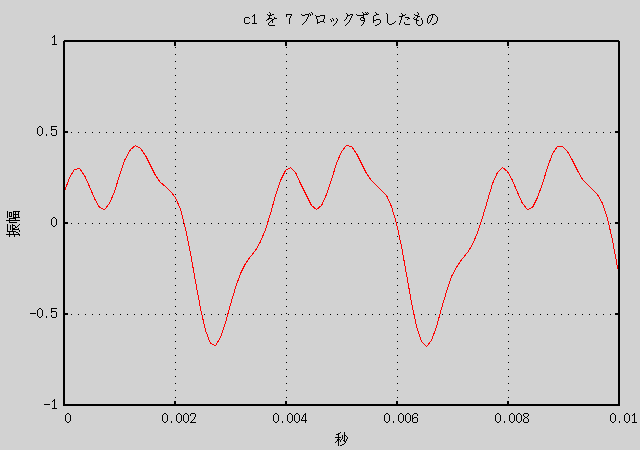


グラフを見ればわかりますが、音声データの形自体はだいぶ違います。 しかし、音声の方は音色の違いは全くないように聞こえます (少なくとも私には)。 つまり、音を重ね合わせるときは、 位相のずれは考えずに重ねても人間には同じに聞こえる、 逆に言えば人間は重ね合わされた音の位相のずれまでを認識しているわけではない、 ということになると思います。
よって、フーリエ変換して音声データから各周波数成分 (スペクトル) を取り出す場合、 sin(nx) の係数 an と cos(nx) の係数 bn を別々に評価することは意味がなく、 それらの自乗和の平方根 (いわゆる「パワースペクトル」)
An = (an2 + bn2)1/2を取り出して評価すべきだということになるように思います。
「種々の音律」 で色々な音階 (音律) を紹介しましたが、 そこで紹介している文献や、以下の本によれば、 現在標準的に使われている半音を、さらに半分にした 1/4 音 (「微分音」) という音程も存在します。
どんな風に聞こえるのか気になったので、その音階を作ってみました。 C (ド) から上のオクターブまでのすべての半音階 (12 + 1 音) と、 すべての微分音 (24 + 1 音) の上昇音階を以下に置きます (1ch, サンプリング周波数 11025Hz の WAV データ)。
微分音を入れると、音と音の音程の違いがかなり微妙になるので、 音階というよりは滑らかに上がっているようにも聞こえます。 上記の本には微分音を使った曲が紹介されているのですが、 どのように聞こえるのでしょうか。
なお、上の音階は平均律を元に、 公比 21/24 の等比数列の周波数の音を作成したのですが、 一般に 21/N の等比数列の周波数の音階は どのように聞こえるのかも少し気になりましたので、 同様に作ってみました。
通常の平均律の音階の音の周波数と同じ音を使うことになるのは、 2, 3, 4, 6, 12 等分の音階のみで、 2 等分は「ド (C0)、ファ♯ (F#0)、ド (C1)」、 3 等分は「ド (C0)、ミ (E0)、ソ♯ (G#0)、ド (C1)」、 4 等分は「ド (C0)、レ♯ (D#0)、ファ♯ (F#0)、ラ (A0)、ド (C1)」、 12 等分は通常の半音階となります。 しかし実際に聞いてみると、 意外に他の音階もそれなりに普通の音階のように聞こえなくもなく、 11 等分と 12 等分と 13 等分もあまり違いはわからないまま 音が一つ足りなかったり、一つ多かったりするように感じます。 平均律と純正律もそうですが、脳は少しの周波数の違いは許容して、 むしろ聞きなじみのある音だと認識しようとしているような気がします。
楽曲では、「短音階」や「長音階」、「四七抜き音階」
などが広く利用されていますが、
現代音楽では等間隔の半音階を対等に扱う「12 音階」を利用した
「十二音音楽」のようなものもあります。
とすると、上のような 12 音にこだわらない分数音階を利用した音楽も
ありうるのかなと思いますが、
これらの音階を再現できる楽器はフレットのない弦楽器や
トロンボーンのような楽器に限定されてしまいますし、
通常の音の位置と違う場所に手を合わせないといけないので、
もしそういう曲があったとしても
電子楽器以外での演奏は難しいかもしれません。
(02/26 2016)
追加です。上の分数音階のうち、7 等分の 8 音階 (seq-7.wav)は、 現在の長音階である「ド、レ、ミ、ファ、ソ、ラ、シ、ド」 の音階に、ある意味で音の数では対応しています。 実際、上の音階を聞いてみると、ややずれている音があるものの、 長音階に似ているように聞こえてしまいます。 特に最初の 3 音は普通の「ド、レ、ミ」のように聞こえます。 これを「等分音階」と呼んでみることにします。
実際には、 長音階ではミとファの間とシとドの間が他の間隔より狭く、 短音階ではレとミの間とソとラの間が他の間隔より狭くなっています。 等分音階ではすべての音の間隔が等分になっていますので、 例えば長音階と同じように聞こえる最初の 3 音でも、 すでに長音階よりは周波数が下がっていて、長音階のレ、ミは
ですが、等分音階の「レ」「ミ」、すなわち等分音階の 2 つ目、3 つ目の音は
となり、長音階とは多少ずれていることがわかります。 周波数をすべて上げてその差も見ると、以下のようになります。
| 音階 | ド | レ | ミ | ファ | ソ | ラ | シ | ド |
|---|---|---|---|---|---|---|---|---|
| (1)長音階 | 261.6Hz | 293.7Hz | 329.6Hz | 349.2Hz | 392.0Hz | 440.0Hz | 493.9Hz | 523.3Hz |
| (2)等分音階 | 261.6Hz | 288.9Hz | 318.9Hz | 352.1Hz | 388.8Hz | 429.2Hz | 473.9Hz | 523.3Hz |
| (1)-(2) | 0.0Hz | 4.8Hz | 10.7Hz | -2.9Hz | 3.2Hz | 10.8Hz | 20.0Hz | 0.0Hz |
等分音階を聞いて一番違和感を感じるのは「ファ」と「シ」だろうと思いますが、 「シ」は確かに一番ずれが大きいものの、 意外に「ファ」のずれはなく、 むしろ「ミ」や「ラ」の方が長音階とのずれはかなり大きくなっています。 音階として並べると前の音との相対的な違いを聞いてしまうので、 そのように感じるのだろうと思われます。
この 7 等分の「ドレミ」で、 簡単な音楽 (チューリップ、きらきら星) を作ってみました。 違いがわかるでしょうか。比較のために、長音階のもの、 および左右のチャンネルに結合したものを以下に置きます。
実は、いずれも一番違いが大きい「シ」の音が含まれていませんので、
等分音階でもそれほど違和感を感じないと思います。
結合するとはっきりうなりが聞こえますが意外に普通です。
これは、多分脳が多少補正をして、
聞きなじみのある音程だと認識しようとしているためではないかと思います。
(02/29 2016)
最近 (といってもここ数ヶ月の話ですが)、 テレビで 2 回ほど「ペンデュラムウェーブ」というものを目にしました。 それは、12 個位の振り子を、少しずつ長さ (すなわち周期) を変えて 並べてぶらさげたもので、 同時に振らせるとその周期が徐々にずれていって、 最初は sin カーブのような形になり、そこからバラバラになって、 あるときにそのいくつかずつがぴたっと揃ったり、 またばらばらになったり、を繰り返す、というものです。 「ペンデュラムウェーブ」で検索すると、動画などもたくさん見つかります。
例えば、周期 1 の振り子、つまり行って帰ってくるまでの時間が 1 の振り子に 対して、周期が 60/59, 60/58, 60/57 の振り子を同時に左から振らせると、
のようになります。よって、この 4 つだと、30 秒後に 2 つずつが揃い、 全部が揃うのは 60 秒後、のようになるわけです。
一般に、周期 60/H1 と周期 60/H2 の振り子は、T 秒後にはそれぞれ T*H1/60 回と T*H2/60 回振れ、よってこの差 T*(H1-H2)/60 が整数であれば その 2 つの振り子が T 秒後に揃うことになります。 H1, H2 が整数であれば、T=60 のときには全部揃いますが、 T が 60 より小さくても、それが 60 の約数 M (= 30, 20, 15, 12, 10, 6, 5, 4, 3, 2) を含んでいれば、 H1-H2 が 60/M を約数に持てば T*(H1-H2)/60 が整数になるので、 それで 60 より短い時間でも揃う、ということになります。
さて、ここではこのペンデュラムウェーブを、 「音」で再現したらどうなるかということを考えてみました。 以下のような波のように音程が高低する音を一つの振り子と考えてみます。
これは、gnuplot と tbl2snd (または tbl2wav) で簡単に作ることができます。 基本的には sin(a*x) のグラフを書かせて、それを table 出力させて、 tbl2snd にかけるだけです。
gnuplot で複数の sin のグラフを書かせて、 それを table 出力させれば、 まさに音のペンデュラムウェーブができます。 以下にサンプルを上げます。 なおサンプルは、振り子の数を 3 個、6 個、12 個にした 3 種類に対して、 60 秒版のものと周期を倍にした 120 秒版のもの、 および音色を全部同じにしたものと、音色を振り子毎に変えてみたものの 4 種類、合計 12 種類を作成しましたが、 さらに、周期を 60/60 から 60/59, 60/58, ... のように増やしたものと、 60/60 から 60/61, 60/62, ... のように減らしたものの 2 種類、 総計 24 種類を作成しました。
グラフは以下の通りです。

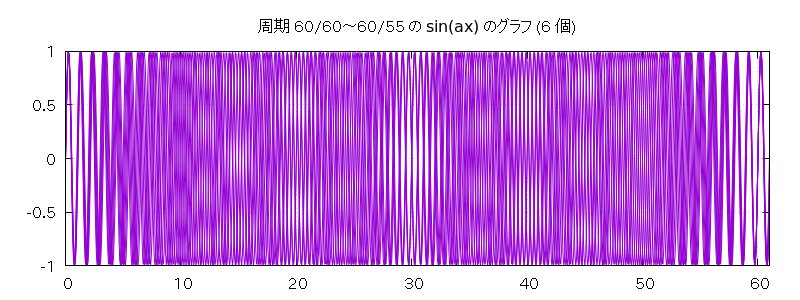
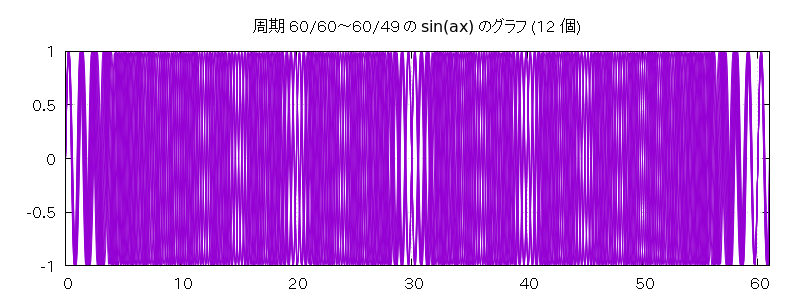
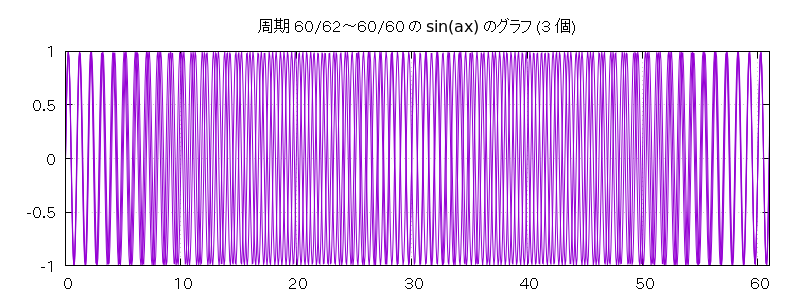


| 音色が全部同じ (60 秒) | 音色が全部同じ (120 秒) | 音色が違う (60 秒) | 音色が違う (120 秒) | |
|---|---|---|---|---|
| 周期 60/60 ~ 60/58 の振り子 3 個 | pnd1-n3-u2-s60.wav | pnd1-n3-u2-s120.wav | pnd1-n3-u1-s60.wav | pnd1-n3-u1-s120.wav |
| 周期 60/60 ~ 60/55 の振り子 6 個 | pnd1-n6-u2-s60.wav | pnd1-n6-u2-s120.wav | pnd1-n6-u1-s60.wav | pnd1-n6-u1-s120.wav |
| 周期 60/60 ~ 60/49 の振り子 12 個 | pnd1-n12-u2-s60.wav | pnd1-n12-u2-s120.wav | pnd1-n12-u1-s60.wav | pnd1-n12-u1-s120.wav |
| 周期 60/62 ~ 60/60 の振り子 3 個 | pnd1+n3-u2-s60.wav | pnd1+n3-u2-s120.wav | pnd1+n3-u1-s60.wav | pnd1+n3-u1-s120.wav |
| 周期 60/65 ~ 60/60 の振り子 6 個 | pnd1+n6-u2-s60.wav | pnd1+n6-u2-s120.wav | pnd1+n6-u1-s60.wav | pnd1+n6-u1-s120.wav |
| 周期 60/71 ~ 60/60 の振り子 12 個 | pnd1+n12-u2-s60.wav | pnd1+n12-u2-s120.wav | pnd1+n12-u1-s60.wav | pnd1+n12-u1-s120.wav |
聞いてみるとわかりますが、 見た目のペンデュラムウェーブにはかなり劣ります。 音が 1 次元的 (音程の高低) な現象で、 見た目の、少なくとも 2 次元的な効果 (左右と前後) が得られにくいのが多分その原因だと思います。
なお、上の音声ファイルは、 例えば上の pnd1-n6-u2-s60.wav であれば、 最近の gnuplot で以下のようにすればできます。
set term wxt size 800,300
unset key
set xrange [0:61]
set ytics 0.5
set sample 1000
plot for [j=1:6] sin(2*pi*(60-j+1)*x/60) w l lt 1
set table "test1.tbl"
replot
unset table
tbl2snd -wav -l60000 -m1 -u2 test1.tbl > pnd1-n6-u2-s60.wav
ギターやバイオリンなどの弦楽器は、 いずれも長さ L の弦を指で押さえることで短くし、 それで弦の振動する周波数 = 音程を変更していますが、 バイオリンやチェロ等とギターには少し構造に違いがあります。
バイオリンやチェロなどは、平らな板の少し上の空間に弦が張ってあるだけで、 押さえる指の位置は任意なので、いくらでも中間の音が出せるのですが (逆に各音階の正しい位置を覚えないと正しい音階が出せない)、 ギターには板の上に「フレット」というでっぱりが 音階に対応する位置に並んでいて、 そのフレットとフレットの間を押さえることで、 容易に正しい音階が出せる仕組みになっています (逆にフレットの位置でほぼ音が固定してしまうので、24 分音などは出せない)。
フレットの位置は等比数列になっています。 半音階の周波数は、公比 21/12 の等比数列
Hn=H・2n/12であり (H は開放弦の周波数)、 弦の長さと周波数は、同じ張り具合 (同じ種類の弦で同じ張力) であれば 反比例の関係にありますので、 Hn に対応するフレットの位置 (= 弦の長さ) Ln は、
Ln=L・2-n/12となります。 1 オクターブ上の音 H12 = 2H のフレット L12 は、L12 = L/2、 すなわち開放弦の半分の長さになります。 ギターも、弦の丁度真ん中の位置に 12 番目のフレットが置かれています。
さて、ここからが本題ですが、本来等比数列であるフレット Ln を、間違えて 12 等分に等間隔に置いた場合 (Rn とする)、 その音程はどのようになるでしょうか。 そのような音程を少し作成してみます。 まず、等間隔なので Rn は、 R0 = L、 R12 = L/2 の等差数列になりますから、
Rn = L - (L/2)・(n/12) = L・(1 - n/24)となり、よって、Rn に対応する周波数 Kn は、
Kn = H/(1 - n/24)となります。これを表にすると以下のようになります。
| n | 音階 | Ln/L | Hn/H | Rn/L | Kn/H |
|---|---|---|---|---|---|
| 0 | ド | 1.0 | 1.0 | 1.0 | 1.0 |
| 1 | ド♯ (レ♭) | 2-1/12=0.944 | 21/12=1.059 | 23/24=0.958 | 24/23=1.043 |
| 2 | レ | 2-2/12=0.891 | 22/12=1.122 | 22/24=0.917 | 24/22=1.091 |
| 3 | レ♯ (ミ♭) | 2-3/12=0.841 | 23/12=1.189 | 21/24=0.875 | 24/21=1.143 |
| 4 | ミ | 2-4/12=0.794 | 24/12=1.260 | 20/24=0.833 | 24/20=1.200 |
| 5 | ファ | 2-5/12=0.749 | 25/12=1.335 | 19/24=0.792 | 24/19=1.263 |
| 6 | ファ♯ (ソ♭) | 2-6/12=0.707 | 26/12=1.414 | 18/24=0.750 | 24/18=1.333 |
| 7 | ソ | 2-7/12=0.667 | 27/12=1.498 | 17/24=0.708 | 24/17=1.412 |
| 8 | ソ♯ (ラ♭) | 2-8/12=0.630 | 28/12=1.587 | 16/24=0.667 | 24/16=1.500 |
| 9 | ラ | 2-9/12=0.595 | 29/12=1.682 | 15/24=0.625 | 24/15=1.600 |
| 10 | ラ♯ (シ♭) | 2-10/12=0.561 | 210/12=1.782 | 14/24=0.583 | 24/14=1.714 |
| 11 | シ | 2-11/12=0.530 | 211/12=1.888 | 13/24=0.541 | 24/13=1.847 |
| 12 | ド | 1/2=0.5 | 2.0 | 1/2=0.5 | 2.0 |
さらにフレットの位置を図にしたものが以下の図です。
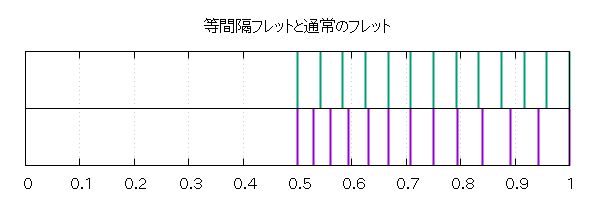
この図からもわかりますが、 真ん中の 6 音位は半音が一つずれた位の音になっていて、 等間隔フレットでは正常な音階にはならず、 最後の 2 音で音程がかなり上がる形になります。 実際に音階にしたものを以下に置きます。
| フレット | 通常 | 等間隔 |
|---|---|---|
| ド | hi0.wav(261.63Hz) | sa0.wav(261.63Hz) |
| ド♯ (レ♭) | hi1.wav(277.18Hz) | sa1.wav(273.00Hz) |
| レ | hi2.wav(293.66Hz) | sa2.wav(285.41Hz) |
| レ♯ (ミ♭) | hi3.wav(311.13Hz) | sa3.wav(299.00Hz) |
| ミ | hi4.wav(329.63Hz) | sa4.wav(313.95Hz) |
| ファ | hi5.wav(349.23Hz) | sa5.wav(330.47Hz) |
| ファ♯ (ソ♭) | hi6.wav(369.99Hz) | sa6.wav(348.83Hz) |
| ソ | hi7.wav(392.00Hz) | sa7.wav(369.35Hz) |
| ソ♯ (ラ♭) | hi8.wav(415.30Hz) | sa8.wav(392.44Hz) |
| ラ | hi9.wav(440.00Hz) | sa9.wav(418.60Hz) |
| ラ♯ (シ♭) | hi10.wav(466.16Hz) | sa10.wav(448.50Hz) |
| シ | hi11.wav(493.88Hz) | sa11.wav(483.00Hz) |
| ド | hi12.wav(523.25Hz) | sa12.wav(523.25Hz) |
特に重ねたものを聞いてみると、両者の音階がだいぶ違うので、 かなり強いうなりがでるのがわかりますが、 単独の等間隔フレット音階、特に半音階のものを聞くと、 脳内で多少の補正が入るのか、あまり違和感がないがなく聞こえてしまいます。 短音階の場合は、最後に半音 2 つ分上がりますが、 その最後の部分に一番大きな違いがでるので、 最後のシ♭からドへのジャンプがかなりあるのがわかります。
最後に、例によってチューリップを作ってみました。 単純な音階よりも、曲の方がずれがわかりやすいと思います。 等間隔音階は、最初はミが半音下った短調のチューリップのようですが、 その後もずれがでて、調がよくわからなくなります。
トランペットやホルンなどの金管楽器は、 唇の振動を楽器内で共鳴させることで音を出しますが、 音程の変化は、バルブを使って息の通る長さを変える (長くする) ことで行っています。 しかし、バルブは基本的には 3 つしかなく、
という仕組みになっているだけで、 その組み合わせでは半音を 0 ~ 6 つ分下げることしかできません。 その他の音階は「自然倍音」を利用して吹いています。
金管楽器は、バルブを使わなくても唇の振動の具合などを変えることで、 いくつかの種類の音程を出すことができます。 これを「自然倍音」といいます。
高校の物理の「気柱の共鳴」で、
という話を学びます (L は管長、c は音速)。 この n によって変化する周波数がまさに自然倍音です。 バルブを使わなくても、 それらの周波数の音は共鳴して大きくなりやすい音なので、 色々な周波数の音が出ます。
フルートは開管構造なので開管の自然倍音列がでますし、 オーボエや金管楽器では楽器の構造は閉管ですが、 直管でなく出口が広くなっていたり、 円錐のように徐々に広がっていく構造になっているために やはり開管の自然倍音列がでるようです。 一方クラリネットは閉管の自然倍音列がでるようです。
実際に n=1 から n=16 までで、 自然倍音列はどのような音なのかを作ってみました。 音程の表と合わせて紹介します。 なお、自然倍音は、完全に正しい音階に当てはまった音がでるわけではありません。 それを以下のように数値化して表で示します。
C1, C#1, D1, D#1, E1, F1, F#1, G1, G#1, A1, A#1, B1, C2となる。
| 開管 | 閉管 | |||||
|---|---|---|---|---|---|---|
| n | 周波数 | D(f) | 音名 | 周波数 | D(f) | 音名 |
| 1 | f0=132Hz | 0.00 | C1 | 0.5f0=66Hz | -12 + 0.00 | C0 |
| 2 | 2f0=264Hz | 12 + 0.00 | C2 | 1.5f0=198Hz | 7.02 | G1 |
| 3 | 3f0=396Hz | 12 + 7.02 | G2 | 2.5f0=330Hz | 12 + 3.86 | E2 |
| 4 | 4f0=528Hz | 24 + 0.00 | C3 | 3.5f0=462Hz | 12 + 9.69 | A2 と A#2 の間 |
| 5 | 5f0=660Hz | 24 + 3.86 | E3 | 4.5f0=594Hz | 24 + 2.04 | D3 |
| 6 | 6f0=792Hz | 24 + 7.02 | G3 | 5.5f0=726Hz | 24 + 5.51 | F3 と F#3 の間 |
| 7 | 7f0=924Hz | 24 + 9.69 | A3 と A#3 の間 | 6.5f0=858Hz | 24 + 8.41 | G#3 と A3 の間 |
| 8 | 8f0=1056Hz | 36 + 0.00 | C4 | 7.5f0=990Hz | 24 + 10.88 | B3 |
| 9 | 9f0=1188Hz | 36 + 2.04 | D4 | 8.5f0=1122Hz | 36 + 1.05 | C#4 |
| 10 | 10f0=1320Hz | 36 + 3.86 | E4 | 9.5f0=1254Hz | 36 + 2.98 | D#4 |
| 11 | 11f0=1452Hz | 36 + 5.51 | F4 と F#4 の間 | 10.5f0=1386Hz | 36 + 4.71 | F4 |
| 12 | 12f0=1584Hz | 36 + 7.02 | G4 | 11.5f0=1518Hz | 36 + 6.28 | F#4 |
| 13 | 13f0=1716Hz | 36 + 8.41 | G#4 と A4 の間 | 12.5f0=1650Hz | 36 + 7.73 | G#4 |
| 14 | 14f0=1848Hz | 36 + 9.69 | A4 と A#4 の間 | 13.5f0=1782Hz | 36 + 9.06 | A4 |
| 15 | 15f0=1980Hz | 36 + 10.88 | B4 | 14.5f0=1914Hz | 36 + 10.30 | A#4 |
| 16 | 16f0=2112Hz | 48 + 0.00 | C5 | 15.5f0=2046Hz | 36 + 11.45 | B4 と C5 の間 |
自然倍音は、低い音は音程の間隔が広く、高い音は間隔が狭くなっています。 特にかなり上の方は開管自然倍音も怪しげな音が多くなってきます。
ホルンやトランペットには昔はバルブがなく、 その頃はトランペットは制限された音階のみのファンファーレや 合図のような曲しか演奏できませんでしたが、 ホルンは管が長いためにトランペットよりは 1 オクターブ上 (実際には f0 は半オクターブ位の違い) の自然倍音を使うことができたため、 ホルンの方がバルブなしでも途中の細かい音程まで出せ、 さらに手を出口の方に入れて半音や全音下げる 「ストップ奏法」なども編み出されたため、 バルブがなくてもほぼすべての音階の音が出せていました。 ちなみに、現在バルブのあるホルンでも手を出口に入れるのはその名残りです。
バルブのないホルンは「ナチュラルホルン」といって、 現在でも演奏に使われることもありますが、 正しく吹くのはかなり難しいそうです。
なお、上の表の D(f) のずれの小数部分を 100 倍した (%) 値を
「セント」と呼ぶことがあります。例えば、n=3 の閉管倍音は、
E2 とは -14 セントのずれ、となります。
(01/05 2021)
すみません、最後のセントの説明がわかりにくいので補足説明します。
E2 の D(f) 値は 12 + 4.00 なので、
n=3 の閉管倍音の D(f) 値と E2 の D(f) 値との差は、
(12 + 3.86) - (12 + 4.00) = -0.14 となります。
それを 100 倍した値の単位がセントです。
だから、-14 セントのずれ、となります。
(06/13 2023)
ここでは、金管楽器の自然倍音に関する実験として、 ホルンとホースの自然倍音の周波数を測定して考察してみました。 詳しくは、以下をご覧ください。
注意: 今 (2025) 見ると、やや用語が変です。「パワースペクトル」
と書いてあるのは正しい使い方ではなく、「振幅スペクトル」と書くべきでした。
また、データを FFT にかけるときも、
左右の音声データを実部・虚部に流してスペクトルを求めればよかったのですが、
そうせずに実数データとして流した 2 つの複素数データの平均を考えているので、
やや不適切だったと思いますが、結果はほぼ変わらないと思います。
時間ができたら、少し改訂したいと思います。
(07/24 2025)
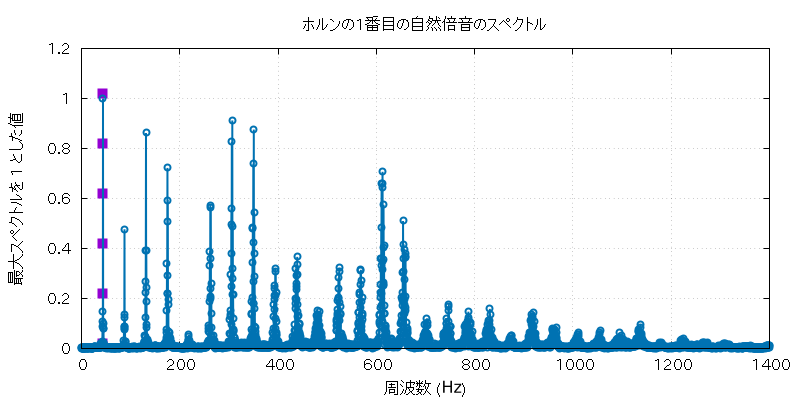
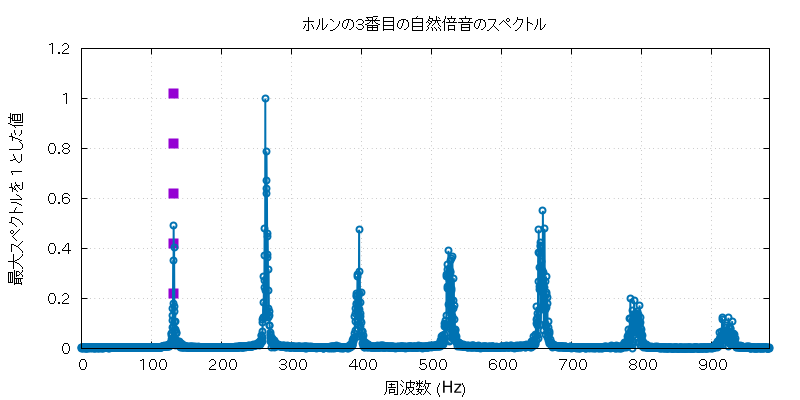
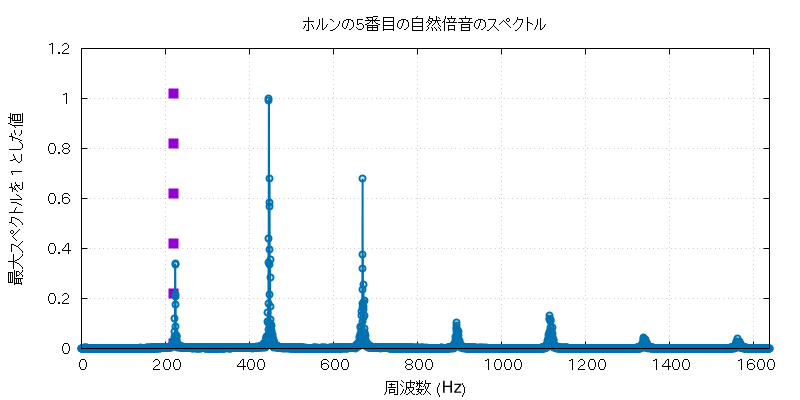
以下に、この実験で使用したホルンとホースの自然倍音全部の音 (の FFT に使用した部分) と、 その FFT にかけた全グラフを置いておきます。
| 自然倍音 | 実音データ |
|---|---|
| fH1 | sub-1.wav |
| fH2 | sub-2.wav |
| fH3 | sub-3.wav |
| fH4 | sub-4.wav |
| fH5 | sub-5.wav |
| fH6 | sub-6.wav |
| fH7 | sub-7.wav |
| fH8 | sub-8.wav |
| fH9 | sub-9.wav |
| fH10 | sub-10.wav |
| fH11 | sub-11.wav |
| fH12 | sub-12.wav |
| fH13 | sub-13.wav |





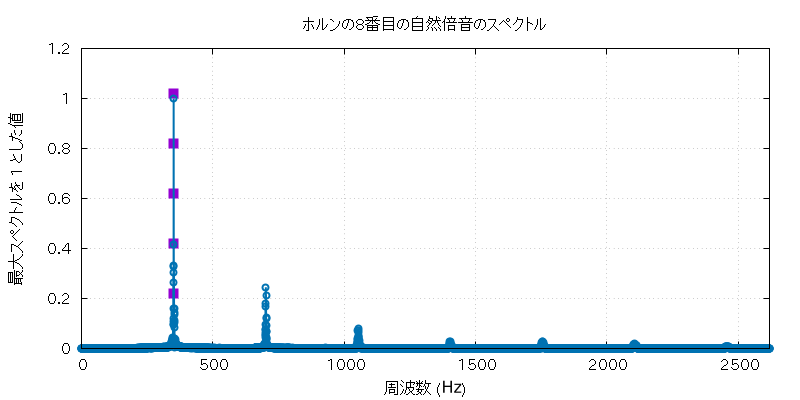
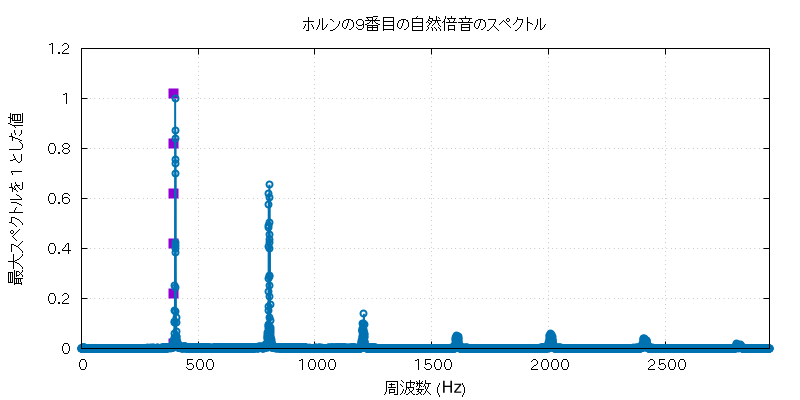
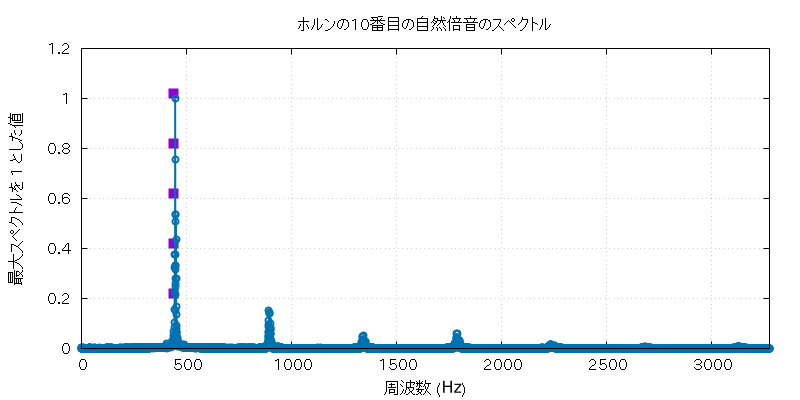
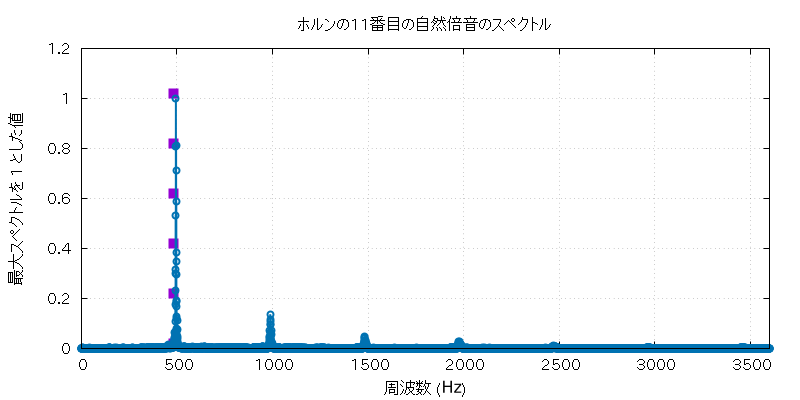

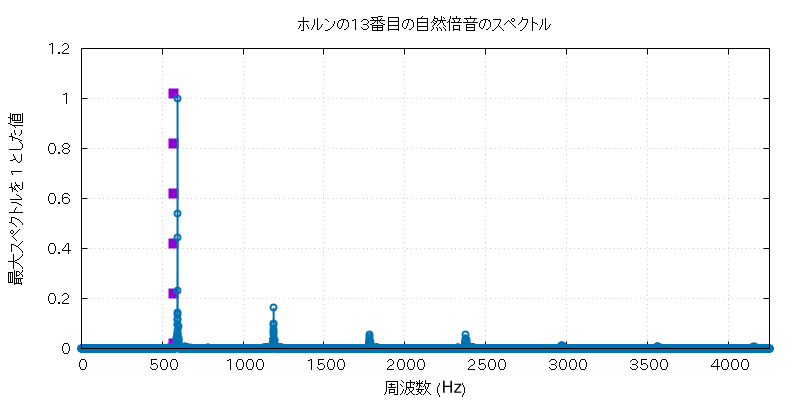
| 自然倍音 | 実音データ |
|---|---|
| fh1 | sub-1.wav |
| fh2 | sub-2.wav |
| fh3 | sub-3.wav |
| fh4 | sub-4.wav |
| fh5 | sub-5.wav |
| fh6 | sub-6.wav |
| fh7 | sub-7.wav |
| fh8 | sub-8.wav |
| fh9 | sub-9.wav |
| fh10 | sub-10.wav |
| fh11 | sub-11.wav |
| fh12 | sub-12.wav |
| fh13 | sub-13.wav |
| fh14 | sub-14.wav |
| fh15 | sub-15.wav |
| fh16 | sub-16.wav |
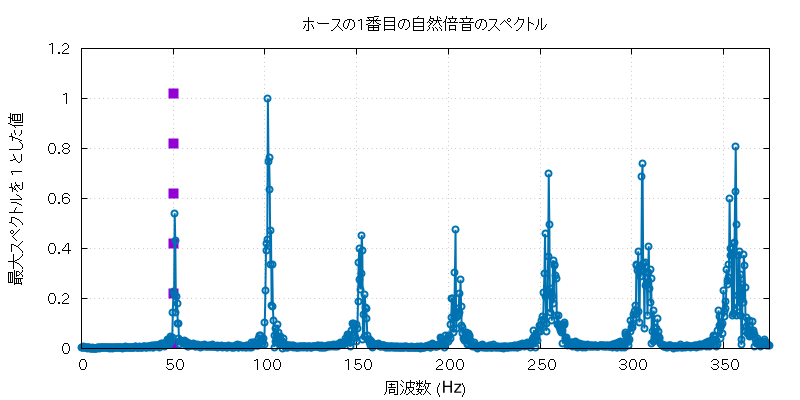

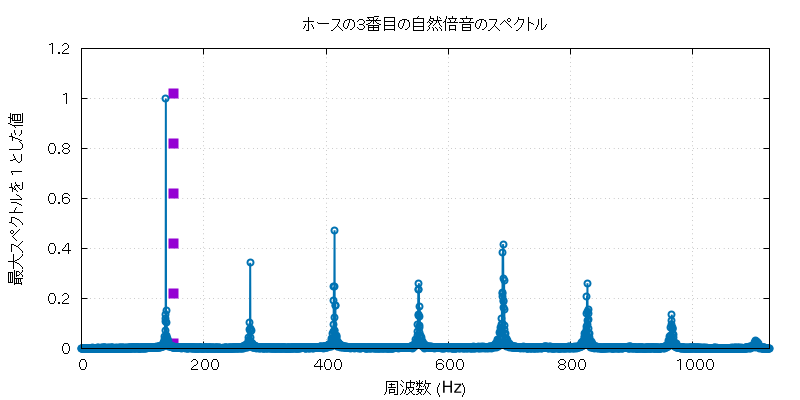
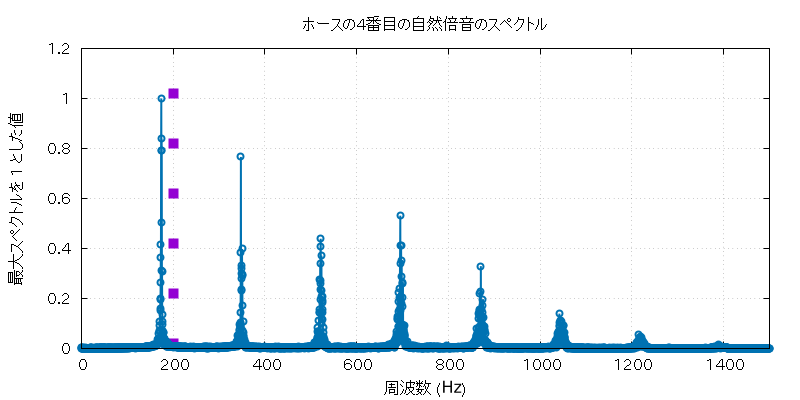
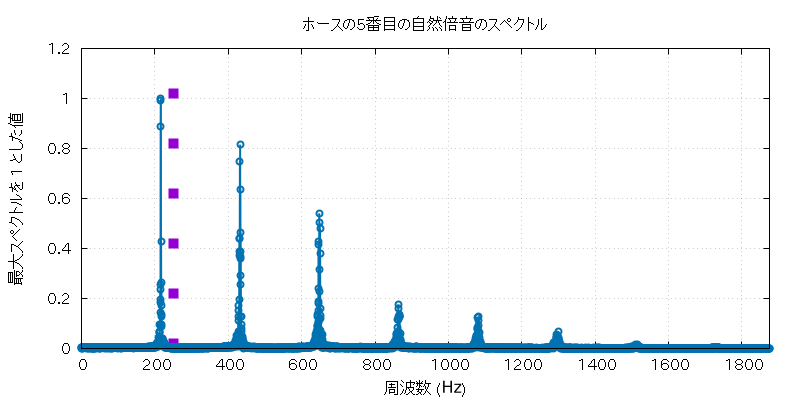
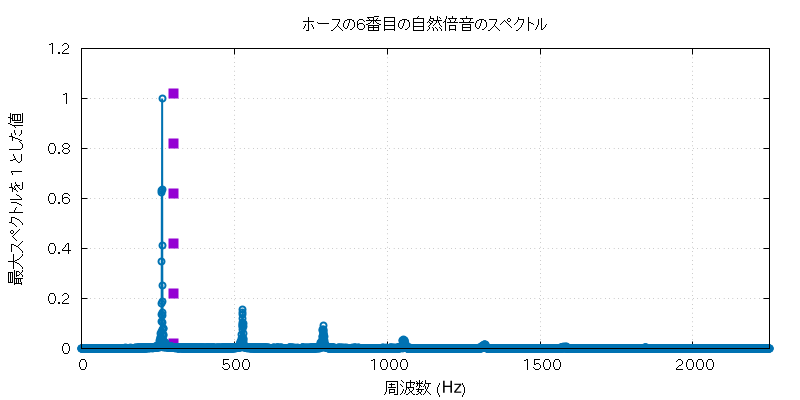
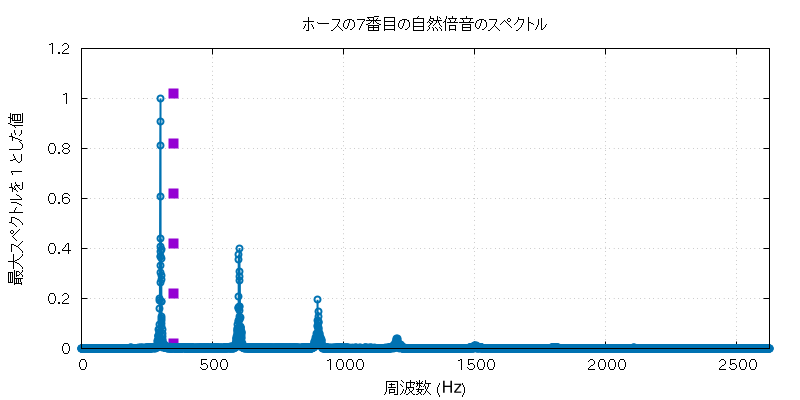
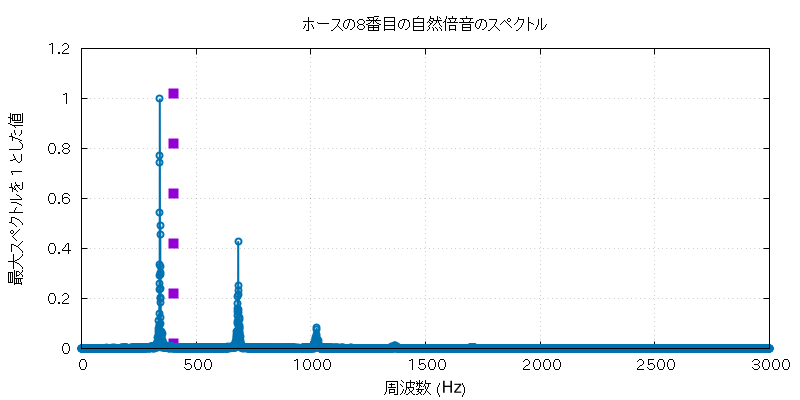
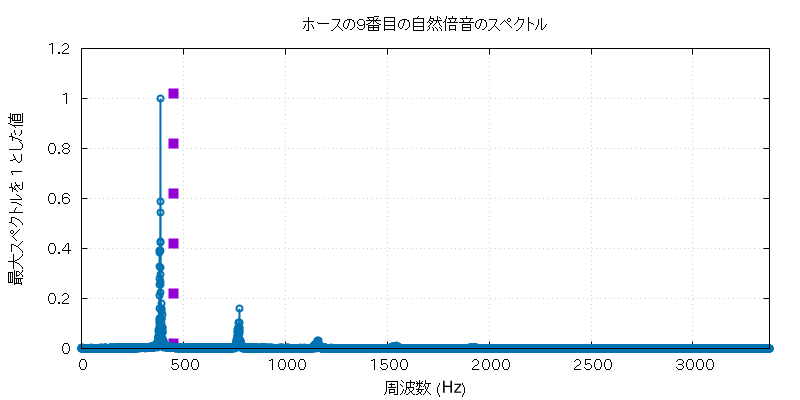
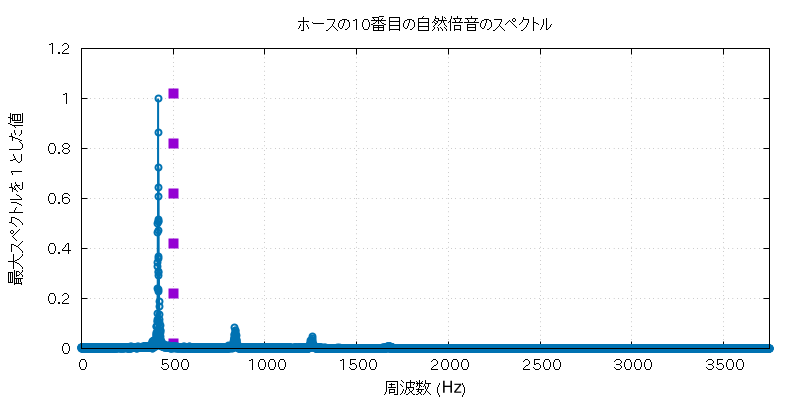


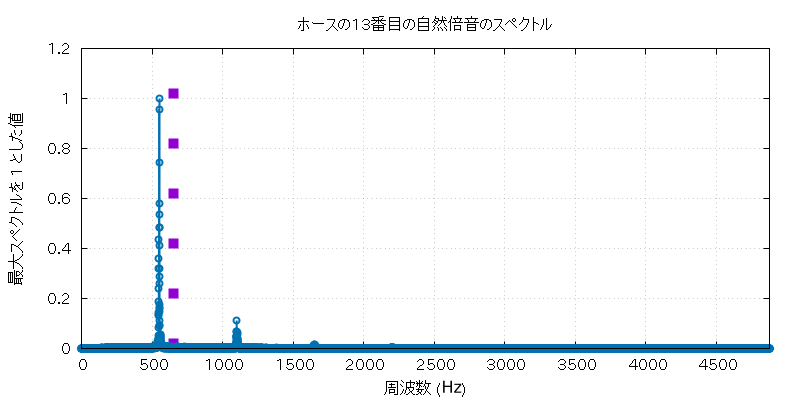
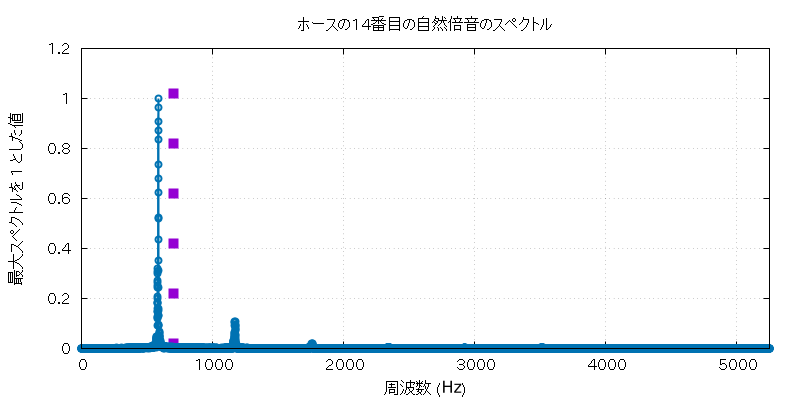
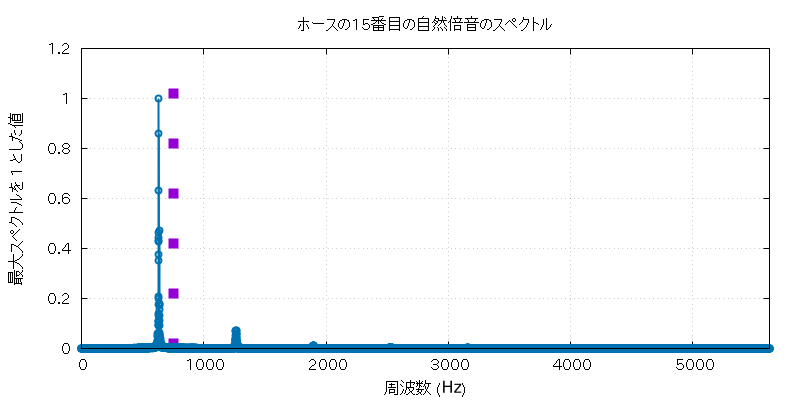
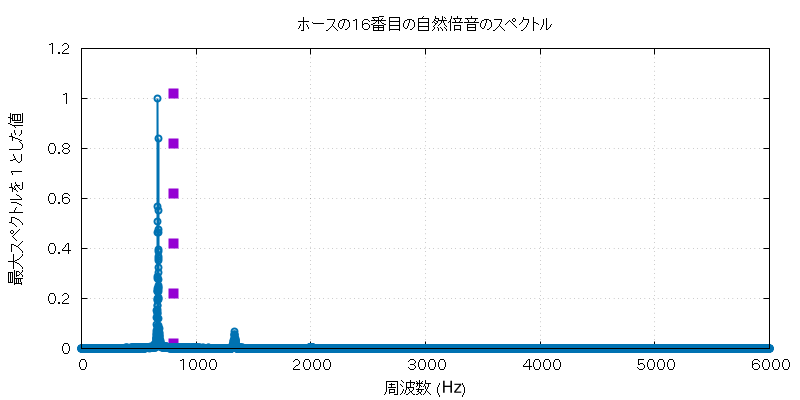
| 高低 | 実音データ |
|---|---|
| 中 | sub-1.wav |
| 低め | sub-2.wav |
| 高め | sub-3.wav |
| 高め | sub-4.wav |
| 低め | sub-5.wav |
| 高め | sub-6.wav |