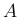
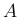 に関する場合分けをして考えていく。
本節では、まず
に関する場合分けをして考えていく。
本節では、まず 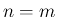 で
で 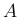 が正則、すなわち
が正則、すなわち 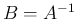 が存在する場合を
考える。
が存在する場合を
考える。
この場合、(4) は、
と変形できる。
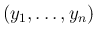 の分布関数
の分布関数
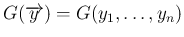 は、
は、
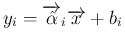 、
および
、
および
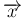 の密度関数
の密度関数
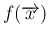 を用いてこれは、
の形に書くことができる。
この積分を (11) で変数変換すると、
そのヤコビ行列式は、
を用いてこれは、
の形に書くことができる。
この積分を (11) で変数変換すると、
そのヤコビ行列式は、
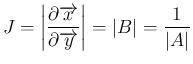
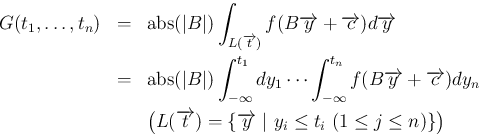
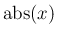 は
は 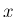 の絶対値とする。
の絶対値とする。
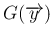 を
を
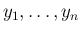 で微分したものが
で微分したものが
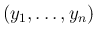 の密度関数
の密度関数
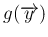 となるので、
となる。よって、
となるので、
となる。よって、
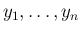 が独立であることは、
この
が独立であることは、
この
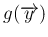 が、各
が、各 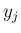 の関数の積に書けることと同値になる。
の関数の積に書けることと同値になる。
(9) より、
となるが、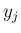 の関数の積になることは、
の関数の積になることは、
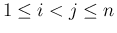 となるすべての
となるすべての 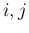 に対して
に対して 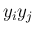 の係数
の係数 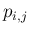 が 0 になることと同値になる。
そしてそれは、
が 0 になることと同値になる。
そしてそれは、
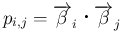 より、
より、
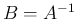 の列ベクトル
の列ベクトル
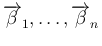 が
互いに垂直であることを意味する。
この場合はこれが
が
互いに垂直であることを意味する。
この場合はこれが
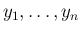 の独立性の条件となる。
の独立性の条件となる。
この 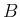 の列ベクトル
の列ベクトル
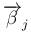 に関する条件を、
元の行列
に関する条件を、
元の行列 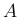 に関する条件に書き直す。
に関する条件に書き直す。
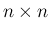 行列
行列 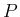 が
が 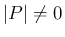 で、その逆行列を
で、その逆行列を 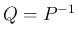 とし、
とし、
![$\displaystyle P=\left[\begin{array}{c}\overrightarrow{\hat{p}}_1\\ \vdots\\ \ov...
...array}{ccc}\overrightarrow{q}_1&\cdots&\overrightarrow{q}_n\end{array}\right]
$](img79.png)
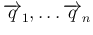 が互いに垂直であることと、
が互いに垂直であることと、
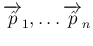 が互いに垂直であることは同値。
が互いに垂直であることは同値。
証明
![$PQ = \left[\overrightarrow{\hat{p}}_i\overrightarrow{q}_j\right]_{n,n}=E$](img82.png) より
より
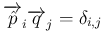 となるから、
となるから、
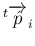 は
は
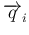 以外の
以外の
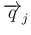 すべてに垂直、
すべてに垂直、
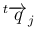 は
は
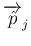 以外の
以外の
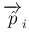 すべてに垂直、となる。
すべてに垂直、となる。
よって、今
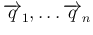 が互いに垂直であるとすると、
が互いに垂直であるとすると、
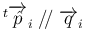 となり、
となり、
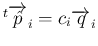 と書け、
と書け、
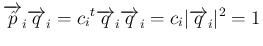
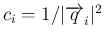 となる。よって、
となる。よって、
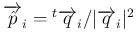 (
(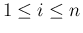 ) は
互いに垂直となる。逆も同様。
) は
互いに垂直となる。逆も同様。
この命題 1 より、
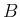 の列ベクトルの垂直性は
の列ベクトルの垂直性は 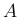 の行ベクトルの垂直性と同値になる。
結局、
の行ベクトルの垂直性と同値になる。
結局、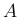 が正則な場合は、
が正則な場合は、
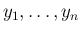 が独立であることは、
A の行ベクトル
が独立であることは、
A の行ベクトル
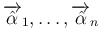 が
互いに垂直であることが条件となる。
が
互いに垂直であることが条件となる。
例えば、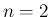 の場合、
の場合、
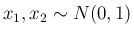 が独立であり、
が独立であり、
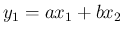 ,
, 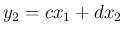 で
で 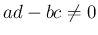 の場合、
の場合、
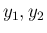 が独立であることは、
が独立であることは、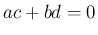 と同値となるので、
と同値となるので、
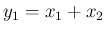 と
と 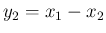 は独立、
は独立、
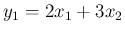 と
と 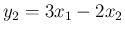 は独立だが、
は独立だが、
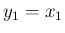 と
と 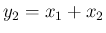 は独立ではない。
は独立ではない。
竹野茂治@新潟工科大学