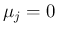
![[*]](crossref.png) を証明する。
なお、
を証明する。
なお、![[*]](crossref.png) 節最後に述べたように、
節最後に述べたように、
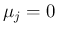 ,
, 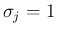 ,
, 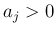 として考える。
として考える。
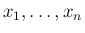 は独立なので、
は独立なので、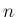 次元確率変数
次元確率変数
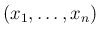 の
密度関数
の
密度関数
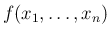 は
は
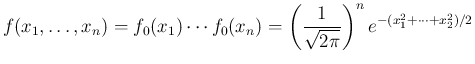
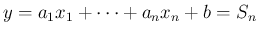 の分布関数
の分布関数 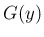 は、
は、
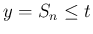 を
を 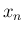 について書けば
について書けば
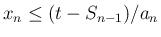 と
なるので、
と
なるので、
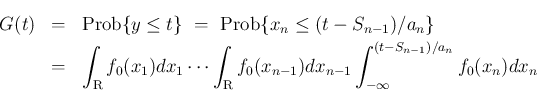
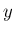 の密度関数
の密度関数 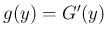 は、
は、
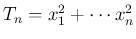 とする。
とする。
この指数の部分は、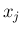 にする 2 次式で、
にする 2 次式で、
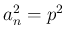 と書くことにすれば、それを
と書くことにすれば、それを 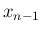 について整理すると、
について整理すると、
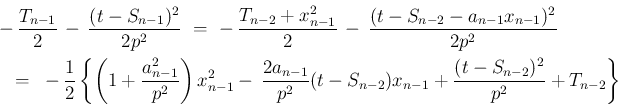
![[*]](crossref.png) を用いれば、
を用いれば、
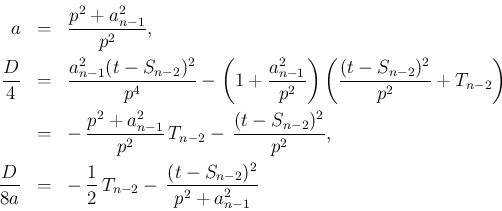
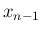 での積分の結果は、
となる。これと、積分前の
での積分の結果は、
となる。これと、積分前の
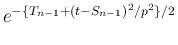
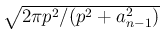 倍され、
指数部分は
倍され、
指数部分は 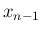 の項が消え、代わりに
の項が消え、代わりに 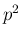 に
に 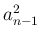 が
追加されることがわかる。
が
追加されることがわかる。
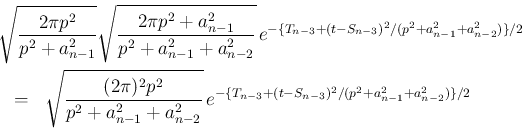
これを続けていけば、最後の 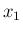 での積分の結果
での積分の結果 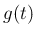 は、
は、
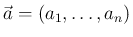 とすれば、
とすれば、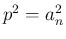 より以下のようになる。
より以下のようになる。
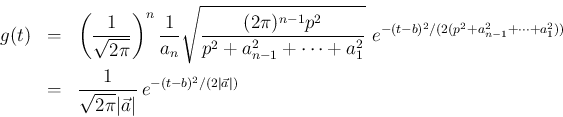
 の密度関数
の密度関数 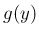 が
正規分布
が
正規分布
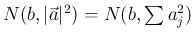 の密度関数に等しいことを
意味し、
これで
の密度関数に等しいことを
意味し、
これで 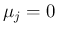 ,
, 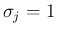 の場合の命題
の場合の命題 ![[*]](crossref.png) が
示されたことになる。
が
示されたことになる。
竹野茂治@新潟工科大学