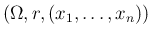
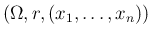 を
を 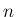 次元離散分布、
次元離散分布、
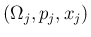 (
(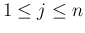 ) をその周辺分布とする。
すべての
) をその周辺分布とする。
すべての
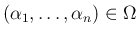 に対し
に対し
が成り立つとき、確率変数
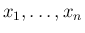 は「独立」であるという。
は「独立」であるという。
(6) は、
と表すこともできる。
逆に、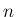 個の確率分布
個の確率分布
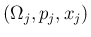 に対して、
(7) で
に対して、
(7) で 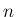 次元確率関数
次元確率関数 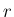 を定義すれば、
これは当然 (4),(5) を
満たすので、ひとつの
を定義すれば、
これは当然 (4),(5) を
満たすので、ひとつの 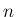 次元確率分布が決定し、
その元ではこの確率変数
次元確率分布が決定し、
その元ではこの確率変数
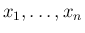 は独立になる。
は独立になる。
つまり、確率変数
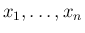 の独立性は、
の独立性は、
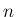 次元確率分布 (
次元確率分布 (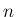 次元確率関数) の元で決まるものであり、
また
次元確率関数) の元で決まるものであり、
また 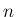 個の確率変数が独立となるような
個の確率変数が独立となるような 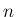 次元確率分布は
いつでも作ることができる。
次元確率分布は
いつでも作ることができる。
竹野茂治@新潟工科大学