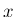
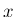 、その値の集合である
標本空間
、その値の集合である
標本空間
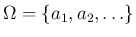 、
および
、
および 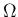 上の確率関数
上の確率関数
![$p:\Omega\rightarrow [0,1]$](img5.png) によって決定する。
ここで、
によって決定する。
ここで、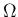 は有限集合かまたは可算集合。
確率関数
は有限集合かまたは可算集合。
確率関数 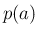 の値は、
の値は、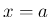 である確率、すなわち
である確率、すなわち
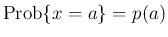
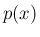 は
を満たす必要がある。
なお、以後
は
を満たす必要がある。
なお、以後
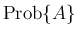 で「
で「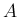 である確率」を表すことにする。
である確率」を表すことにする。
本稿では、この 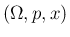 の組を「離散確率分布」と呼ぶことにする。
の組を「離散確率分布」と呼ぶことにする。
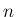 個の離散確率分布
個の離散確率分布
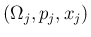 (
(
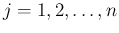 ) に対して、
) に対して、
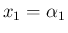 かつ ...かつ
かつ ...かつ 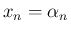 」
となる確率を考えることができるとき、直積集合
を標本空間、
」
となる確率を考えることができるとき、直積集合
を標本空間、
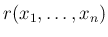 を
を 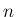 変数の確率関数とする
変数の確率関数とする 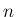 次元確率変数
次元確率変数
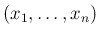 を考えることができる。
この組
を考えることができる。
この組
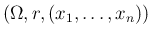 を「
を「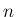 次元離散確率分布」と呼ぶ。
次元離散確率分布」と呼ぶ。
当然 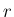 は、
は、
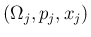 との整合性として、
すべての
との整合性として、
すべての 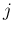 に対して、
も満たす必要がある。
に対して、
も満たす必要がある。
逆に、直積集合 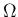 (3) と、
(4) を満たす
(3) と、
(4) を満たす 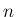 変数
関数
変数
関数
![$r:\Omega\rightarrow[0,1]$](img27.png) を取り、
それに対し (5) の和によって
を取り、
それに対し (5) の和によって 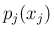 という
関数を定義すれば、条件 (4) により
という
関数を定義すれば、条件 (4) により 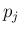 は (1) の条件を満たすので、
は (1) の条件を満たすので、
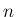 個の離散確率分布
個の離散確率分布
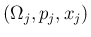 (
(
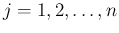 ) が作られ、
) が作られ、
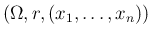 をはその
をはその 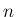 次元離散確率分布となる。
この場合、各離散確率分布
次元離散確率分布となる。
この場合、各離散確率分布
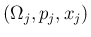 を、
を、
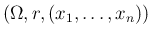 の「周辺分布」と呼ぶことがある。
の「周辺分布」と呼ぶことがある。
竹野茂治@新潟工科大学