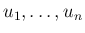
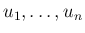 が独立で、
が独立で、
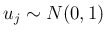 (
(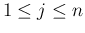 ) の
とき、
) の
とき、
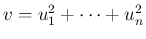 が従う確率分布を
「自由度
が従う確率分布を
「自由度 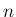 のカイ自乗分布
のカイ自乗分布 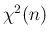 」と呼ぶ。
この
」と呼ぶ。
この 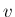 の密度関数
の密度関数 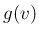 を求める。
を求める。
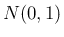 の密度関数を
の密度関数を
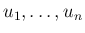 は独立なので、
は独立なので、
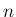 次元確率分布
次元確率分布
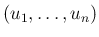 の密度関数は
の密度関数は
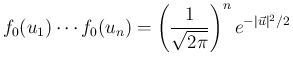
 の分布関数
の分布関数 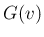 は、
は、
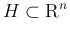 に対して、
に対して、
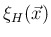 を
を 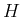 の
定義関数、すなわち
とする。今の場合、
の
定義関数、すなわち
とする。今の場合、
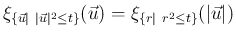
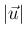 の関数、
すなわち動径方向のみに依存し、よって (14) により、
となり、
の関数、
すなわち動径方向のみに依存し、よって (14) により、
となり、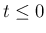 に対しては
に対しては 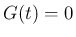 ,
, 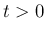 に対しては、
となることがわかる。
よって、
に対しては、
となることがわかる。
よって、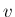 の密度関数
の密度関数 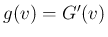 は、
は、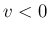 では 0 で、
では 0 で、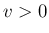 では
では
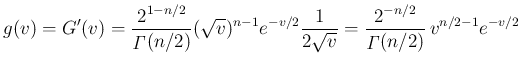
竹野茂治@新潟工科大学