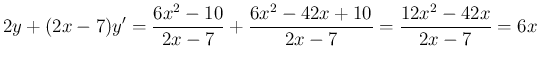4 積の微分による証明
これは、例えば [2] にも書かれている方法であり、
先に積の微分が証明されているとしてそれを用いる方法である。
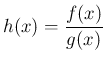 とすると
とすると 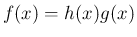 となるので、
積の微分より、
となるので、
積の微分より、
となるから、
を得る、という方法である。
これは極限を必要とせず、比較的容易に導き出せる方法であると思う。
逆にこれを、商の微分の検算に使うことも可能である。
例えば、
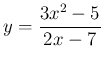
(
1)
の微分を商の微分で
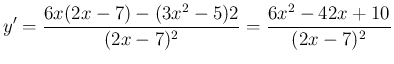
(
2)
と求めた後で、これが合っているかを確認するのに、(1) から
として、この両辺を積の微分で
とした後で、この右辺に (1), (2) を代入して、確かに 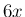 になるかをみる、
という方法である。実際、
になるかをみる、
という方法である。実際、
となるので、
この場合は (2) が正しいことがわかる。
竹野茂治@新潟工科大学
2020-10-21
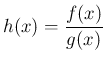 とすると
とすると 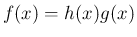 となるので、
積の微分より、
となるので、
積の微分より、
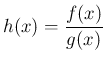 とすると
とすると 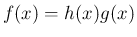 となるので、
積の微分より、
となるので、
積の微分より、
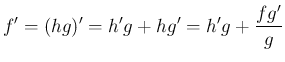
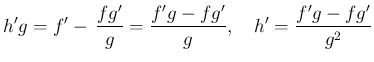
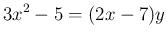
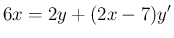
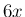 になるかをみる、
という方法である。実際、
になるかをみる、
という方法である。実際、