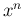 と指数関数、
と指数関数、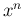 と三角関数の積分の最終形を表す式は、
高校の教科書にも大学の本にも出てこない。
と三角関数の積分の最終形を表す式は、
高校の教科書にも大学の本にも出てこない。
これらは、1 回部分積分を行うことにより、 次数が 1 つ小さい多項式の積の積分に帰着できるため、 その多項式が定数になるまで部分積分を繰り返せば、 いずれ積分が終了する。
もちろん、これで原理的にはどんな場合でも複数回の部分積分を
実際にやれば求まることがわかり、教科書の説明は普通はこれで終わり、
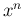 と指数関数、
と指数関数、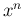 と三角関数の積分の最終形を表す式は、
高校の教科書にも大学の本にも出てこない。
と三角関数の積分の最終形を表す式は、
高校の教科書にも大学の本にも出てこない。
本稿では、部分積分によって漸化式を導くことで、
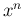 と指数関数の積、
と指数関数の積、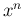 と三角関数の積の積分の具体的な
表現式を作成することを目標とする。
と三角関数の積の積分の具体的な
表現式を作成することを目標とする。
竹野茂治@新潟工科大学