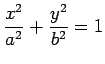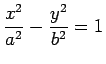3 名前の由来
双曲線関数の名前の由来は、歴史的には詳しくは知らないが、
この関数が双曲線のパラメータ表示になっているからであろう。
良く知られているように、
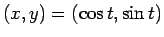 は
は
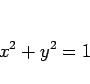
を満たし、この点 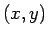 は
は 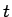 が動くと原点中心で半径 1 の円を描く。
それに対し、
が動くと原点中心で半径 1 の円を描く。
それに対し、
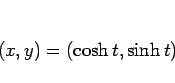 |
(6) |
は、(5) により
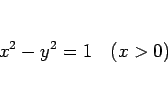
を満たし、よって 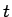 が動くと (6) の点
が動くと (6) の点 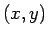 は、双曲線
は、双曲線 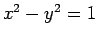 の右半分を描く。
の右半分を描く。
ここで、双曲線とは、
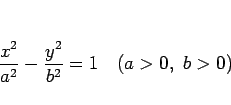 |
(7) |
で表される曲線、あるいはそれを平行移動、回転したものを指す、
いわゆる 2 次曲線の一つである (図 3)。
図 3:
双曲線
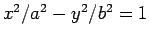 のグラフ
のグラフ
|
|
なお、2 次曲線とは、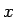 ,
, 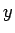 の 2 次式
の 2 次式
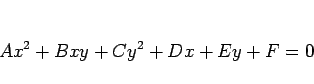
で表される曲線のうち、直線ではないものを指し、
それは適当に平行移動、回転をすると、
次の 3 つのいずれかになることが知られている 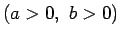 。
。
- 楕円 (ellipse):
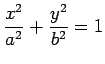
- 放物線 (parabola):
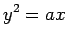
- 双曲線 (hyperbola):
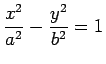
双曲線 (7) の右側は
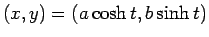 で、
左側は
で、
左側は
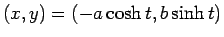 で表されることになる。
で表されることになる。
しかし、それにしても三角関数と双曲線関数は全く物が違うので、
似た名前を用いることに違和感を感じる人もいると思うが、
それはこの後にも出てくる三角関数と双曲線関数の性質の類似性から、
その自然さが徐々にわかってくると思う。
竹野茂治@新潟工科大学
2010年3月19日
![]() は
は